Techniklexikon

Gabelbifurkation

Nichtlineare Dynamik, Chaos, Fraktale, Pitchfork Bifurcation, Kodimension-1-Bifurkation (Bifurkation) eines stabilen Fixpunktes mit Variation eines Parameters m. In diskreten oder kontinuierlichen dynamischen Systemen ist eine Gabelbifurkation nicht generisch, da eine spezielle Symmetrie vorliegen muss. Ein dynamisches System

mit eindimensionalem Parameter m habe bei m = 0 die Ruhelage x^* = 0. Hat die Jacobi-Matrix

nur einen Eigenwert mit Realteil null (eindimensionale Zentrumsmannigfaltigkeit), so wird das Bifurkationsverhalten durch ein eindimensionales dynamisches System erfasst (Abb.). Im Falle der Gabelbifurkation hat dieses reduzierte System die Form . Für  findet man einen stabilen Fixpunkt x^* = 0, der für m > 0 instabil wird, wobei zwei neue symmetrisch gelegene Fixpunkte  entstehen (Abb.). Ein analoges Verhalten existiert auch für iterierte Abbildungen. Liegt die erwähnte Symmetrie nicht vor, so findet man typischerweise eine Tangentenbifurkation (Sattel-Knoten-Bifurkation).

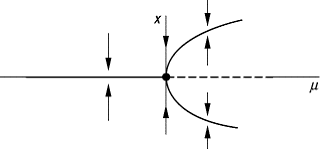
Gabelbifurkation: Das Bifurkationsdiagramm für eine Gabelbifurkation beschreibt Lage und Charakter der beteiligten Fixpunkte als Funktion eines Kontrollparameters m. Der Ort der (des) attraktiven Fixpunkte(s) ist durch volle, die des instabilen Fixpunktes durch gestrichelte Linien gekennzeichnet.