Techniklexikon

Hénon-Heiles-System

Beispiel eines nichtintegrablen mechanischen Systems, das chaotische Bewegung zeigt (deterministisches Chaos). Es wurde 1964 von M. Hénon und C. Heiles angegeben, die die kanonischen Bewegungsgleichungen zur Hamilton-Funktion

untersucht hatten. H beschreibt in kartesischen Koordinaten (q₁, q₂) zwei nichtlinear gekoppelte harmonische Oszillatoren, in Polarkoordinaten (r, q) ein einzelnes Teilchen in einem nicht radialsymmetrishen Potential V(r, q):

Die Arbeiten waren motiviert durch empirische Befunde, nach denen ein Stern, der sich in einem schwach gestörten zylindersymmetrischen Potential bewegt, zusätzlich zur Energie noch eine andere Bewegungskonstante haben sollte. Mit Untersuchungen der Poincaré-Abbildung im Phasenraum des Systems konnten Hénon und Heiles aber zeigen, dass eine solche Konstante nicht existiert, sondern dass die Bewegung im Phasenraum chaotisch ist.

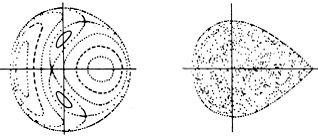
Hénon-Heiles-System: Poincaré-Abbildung.