Techniklexikon

Phasenraum

Thermodynamik und statistische PhysikKlassische Mechanik, Raum eines mechanischen Systems mit f Freiheitsgraden, der von f (verallgemeinerten) Orts- und f Impulskoordinatenachsen aufgespannt wird. Er heisst auch 2f-dimensionaler euklidischer Raum. Der Zustand eines mechanischen Systems wird im Phasenraum durch einen Phasenbildpunkt dargestellt, dessen Koordinaten den Werten der Koordinaten und Impulse , des Systems entsprechen. Der Zustand des mechanischen Systems entwickelt sich längs einer Phasentrajektorie im Phasenraum. Die Eindeutigkeit der Lösungen dieser Gleichungen bedingt, dass durch jeden Phasenraumpunkt höchstens eine Phasenraumtrajektorie gehen kann. Bei periodischen Bewegungen ist die Phasenraumtrajektorie in sich geschlossen. Erhaltungssätze schränken die Mannigfaltigkeit der möglichen Phasentrajektorien eines Systems ein. Jede Erhaltungsgrösse reduziert die Dimension der Mannigfaltigkeit des zugänglichen Phasenraumteils, des sog. Phasenvolumens, also um 1. So bedingt beispielsweise die Energieerhaltung, dass alle erlaubten Phasenraumtrajektorien in der (2f - 1)-dimensionalen Energiehyperfläche des Phasenraumes liegen. In der Quantenphysik ist wegen der Heisenbergschen Unschärferelation  der mechanische Zustand eines Systems, also mithin auch der ihn repräsentierende Phasenraumpunkt, nicht exakt bekannt. Man unterteilt daher zur Charakterisierung des Zustandes den Phasenraum in Zellen des Volumens  und betrachtet die Wahrscheinlichkeitsdichte  in einer solchen Phasenraumzelle, so dass der Erwartungswert einer beliebigen physikalischen Grösse f als  bestimmt werden kann.

In der statistischen Mechanik, für die Beschreibung eines Systems, das aus sehr vielen, gleichartigen Teilchen besteht (z.B. eines Gases), erhält der Phasenraum eine sehr hohe Dimensionalität: jedes Teilchen hat 3 Freiheitsgrade, multipliziert mit der Anzahl von Teilchen pro Mol ergeben sich 3,6 × 10²⁴ Dimensionen. Man spricht in diesem Falle vom G-Raum. In der Näherung eines idealen Gases, bei dem die einzelnen Teilchen nicht miteinander wechselwirken, zerfällt der G-Raum in voneinander unabhängige Teilphasenräume für jedes Molekül, die sog. m-Räume mit nur 3 Freiheitsgraden und 6 Dimensionen für einatomige Gase. Für mehratomige Gase erhöht sich die Anzahl der Freiheitsgrade und damit der Dimensionen des m-Raumes.

Der Phasenraum ist nützlich bei der Untersuchung von Einteilchensystemen, er hat hier nur noch 6 Dimensionen. Die eindimensionale Bewegung eines Einteilchensystems kann mit einem zweidimensionalen Phasenraum mit den Achsen (q, p) beschrieben werden. Ist die Phasentrajektorie des Systems eine geschlossene Kurve, so oszilliert das System, eine periodisch sich wiederholende Phasentrajektorie deutet auf eine periodische Bewegung hin.

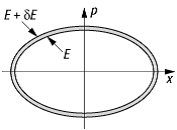
Phasenraum: Klassischer Phasenraum eines eindimensionalen harmonischen Oszillators mit einer Energie zwischen E und E + dE. Der zugängliche Teil ist die Fläche zwischen den beiden Ellipsen.