Techniklexikon

Hamilton-Formalismus für Felder

Quantenmechanik, quantentheoretischer Formalismus im Rahmen der Feldquantisierung. Der Übergang von der nichtgequantelten Wellenfunktion Y(x) zur gequantelten kann unmittelbar durch die Vertauschungsregeln ausgedrückt werden:

Mit Hilfe der gequantelten Wellenfunktion

 lässt sich der Hamilton-Operator darstellen:

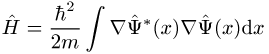
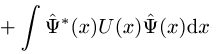
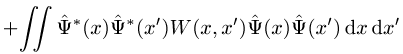
Man kann Y(x) als De-Broglie-Schrödinger-Feld und H als Energie dieses Wellenfeldes auffassen.

Die Theorie der zweiten Quantelung ermöglicht damit die Behandlung der Theorie von Systemen identischer Teilchen, wie hier der Bosonen. Genauso verläuft die Quantelung von Fermionen. Typisch für diese Quantelung ist die Ersetzung des klassischen Feldes Y(x) durch den Operator .