Techniklexikon

Integralgleichungen

Gleichungen zur Bestimmung einer auf dem Intervall  definierten Funktion  mit Hilfe integraler Relationen, d.h. diese Gleichungen enthalten einen von  abhängenden Integranden, z.B.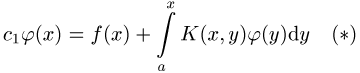

mit einer Störungsfunktion f(x) und einem Kern K(x,y). Im Fall  spricht man von einer Integralgleichung erster Art, andernfalls zweiter Art. Beim Beispiel (*) handelt es sich um eine Volterrasche Integralgleichung; sind beide Integrationsgrenzen konstant, handelt es sich um eine Fredholmsche Integralgleichung (Fredholmsche Alternative).

Für die mathematische Physik bieten Integralgleichungen den Vorteil, dass sie im Gegensatz zu Differentialgleichungen die explizite Einbeziehung von Randbedingungen ermöglichen. Manche Probleme, wie z.B. Streu- oder Transportprobleme, führen notwendigerweise auf Integro-Differentialgleichungen. Andere, wie z.B. die Schrödingergleichung, können mit Hilfe der Fourier-Transformation auf Integralgleichungen transformiert werden.