Techniklexikon

konforme Abbildung

Mathematische Methoden und Computereinsatz, winkel- bzw. orientierungstreue Abbildung. Damit eine Transformation bzw. Funktion diese Eigenschaft haben kann, muss sie holomorph analytisch (analytische Funktion) und ihre Ableitung stets von Null verschieden sein; damit ist die Funktion biholomorph, d.h. umkehrbar stetig differenzierbar. Eine komplexe Funktion  ist genau dann konform (winkel- und orientierungstreu), wenn sie biholomorph ist. Betrachtet man zwei glatte von einem Punkt z₀ der komplexen Zahlenebene ausgehende Wege, d.h. stetig-differenzierbare Abbildungen

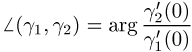mit Tangenten  und Halbtangenten, d.h. Strahlen . Der Winkel zwischen den Wegen  und  ist definiert als der Winkel zwischen den Halbtangenten und ist (bis auf Addition von ganzzahligen Vielfachen von 2) gegeben durch . Ist f eine konforme Abbildung, so gilt für die Bildwege .

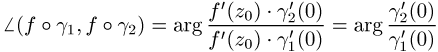Konforme Abbildungen spielen bei vielen Anwendungen der Funktionentheorie, z.B. in der Elektrostatik (Beschreibung des Feldes einer Punktladung, die von einem metallischen Leiter beliebiger Fläche umschlossen wird), Elastizitätstheorie und Strömungslehre eine Rolle. Kennt man z.B. die Strömung S um ein einfaches Objekt, das in der komplexen Zahlenebene das projizierte Profil P besitzt, z.B. einen Kreis, so kann die Strömung  um ein kompliziertes Profil  aus S berechnet werden, wenn man eine Abbildung konstruieren kann, die P auf  abbildet.