Techniklexikon

Legendre-Polynome

, Legendre-Funktionen der ersten Art, zonale Kugelfunktionen, sind Lösungen der Legendreschen Differentialgleichung und bilden ein vollständiges orthogonales Funktionensystem. Die zugeordenten Legendre-Polynome  (Legendre-Funktionen) sind entsprechend Lösungen der zugeordneten Legendreschen Differentialgleichung und treten als Faktor in den Kugelfunktionen auf.  besitzt im Intervall   Nullstellen. Zwischen  und  besteht die Beziehung

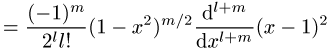
Mit Hilfe von Rekursionsformeln, z.B.

zwischen den Legendre-Polynomen verschiedener Grade lassen sich Polynome höheren Grades auf solche niedrigeren Grades zurückführen und damit z.B. unter Ausnutzung der Orthonormalität Integrale einfacher auswerten.