Techniklexikon

Paralleltransport

Relativitätstheorie und Gravitation eines entlang einer Kurve  (mit Kurvenparameter ) definierten Vektors  liegt genau dann vor, wenn seine kovariante Ableitung entlang der Kurve verschwindet:

Die anschauliche Bedeutung dieses Begriffes entnimmt man der Tatsache, dass in lokalen Inertialkoordinaten (dort ist die kovariante Ableitung gleich der gewöhnlichen) der paralleltransportierte Vektor  im üblichen Sinne parallel verschoben wird. Beispielsweise wird die Tangente entlang einer Geodäten paralleltransportiert. Den Begriff Paralleltransport kann man sofort auf Tensoren beliebiger Stufe verallgemeinern.

Man kann zeigen, dass ein entlang einer geschlossenen Kurve paralleltransportierter Vektor genau dann unverändert bleibt (also wieder in sich selbst übergeführt wird), wenn in der durch die geschlossene Kurve eingeschlossenen Region der Riemannsche Krümmungstensor verschwindet. In diesem Fall ist also der Paralleltransport eines Vektors von einem Ausgangspunkt A zu einem Endpunkt B wegunabhängig und kann, ausgehend von einem nur an einem Raumzeit-Punkt definierten Vektor, zur Konstruktion eines Vektorfeldes verwendet werden.

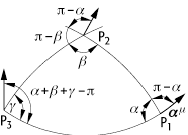
Paralleltransport: Nach Paralleltransport längs des sphärischen Dreiecks P₁P₂P₃ unterscheidet sich der Vektor a^m von Punkt P₁ um a + b + g - p.