Techniklexikon

Stokesscher Integralsatz

Mathematische Methoden und Computereinsatz, ein auf G. Stokes zurückgehender Satz, der einen Zusammenhang herstellt zwischen Volumen- und Oberflächenintegralen bzw. zwischen Integralen auf (p + 1)- und p-dimensionalen Mannigfaltigkeiten. Die äussere Ableitung df einer p-Form f auf einer Mannigfaltigkeit X ist eine (p + 1)-Form (Differentialformen). Ist S eine (p + 1)-dimensionale Untermannigfaltigkeit von X mit Rand ¶S, so gilt:

Identifiziert man speziell im  Vektorfelder und 1-Formen, so folgt für ein Vektorfeld A:

Dabei ist S eine 2-dimensionale Fläche mit Flächenelement da und der von da ausgehenden äusseren Flächennormalen n, ¶S ist die Kurve, die S berandet, dl ein Linienelement darauf.

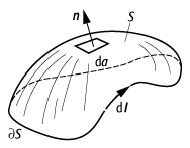
Stokesscher Intergalsatz: im .