Techniklexikon

Differentialformen

Mathematische Methoden und Computereinsatz, antisymmetrische kovariante Tensorfelder auf einer n-dimensionalen Mannigfaltigkeit X. Eine Differentialform f vom Grad p, kurz p-Form, beschreibt an jedem Punkt x Î X eine antisymmetrische p-Linearform

f_x: T_x(X) ´ ... ´ T_x(X)    

(p Faktoren). T_x(X) ist der Tangentialraum von X bei x. Der Raum der antisymmetrischen p-Linearformen auf einem p-dimensionalen Vektorraum ist n!/p!(n - p)!-dimensional für 0 < p < n, sonst p-dimensional. Daher gibt es keine von 0 verschiedenen Differentialformen vom Grad p > n. Es bezeichne  E _p(X) den Raum der glatten p-Formen auf X und  E (X) =  E ₀(X) Å  ...  Å  E _n(X) den Raum aller glatten Differentialformen auf X. Insbesondere ist  E ₀(X) der Raum  C  ^¥ (X) der glatten Funktionen auf X. Durch das äussere Produkt  Ù  wird  E (X) eine Grassmann-Algebra.  Ù  ist assoziativ,

(f Ù y) Ù w = f Ù (y Ù w),

distributiv,

f Ù (y + w) = f Ù y + f Ù w,

und graduiert kommutativ,

f Π E _p(M), y Π E _q(M) Þ f Ù y = ( - 1)^pqf Ù y.

Für f Π E ₀(M) ist

f Ù f = ff,

und für zwei 1-Formen a, b gilt

a Ù b = a ­ b - b ­ a.

Die innere Ableitung    nach einem Vektorfeld  v  ordnet einer p-Form f die (p - 1)- Form  v   f zu, definiert durch

( v   f)( w  ₁, ...,  w  _{p - 1}) = f( v  ,  w  ₁, ...,  w  _{p - 1})

für Vektorfelder  w  _i. Die äussere Ableitung d ordnet einer p-Form eine (p + 1)-Form df zu: Sind x¹, ..., xⁿ lokale Koordinaten und ¶₁, ..., ¶_n die zugehörigen Vektorfelder, so sind die 1-Formen dxⁱ dual zu den ¶_n, d.h. dxⁱ(¶_j) = d_ij (Kronecker-Symbol). Jede p-Form f besitzt eine Darstellung

(unter Verwendung der Einsteinschen Summenkonvention!). Dann ist

Insbesondere gilt für eine 0-Form

und für f Π E _p(X), y Π E _q(X) ist

d(f Ù y) = df Ù y + ( - 1)^pf Ù dy.

Es gilt: d² = 0. f heisst geschlossen, falls df = 0, und exakt, falls f = dy. Die Einschränkung einer geschlossenen Form auf eine hinreichend kleine Umgebung ist exakt. Die Lie-Ableitung von f Π E (X) nach einem Vektorfeld  v  ist

 L  _v  f =  v   df + d( v   f).

Die Lie-Ableitung nach einem Vektorfeld  v  und die innere Ableitung nach einem Vektorfeld  w  erfüllen die wichtige Relation

 L  _v ( w   f) -  w   ( L  _v  f) = [ v ,  w ]  f,

wobei [ v ,  w ] die Lie-Klammer von  v  mit  w  ist. Trägt X eine Orientierung, so kann man p-Formen über p-dimensionale Untermannigfaltigkeiten integrieren (Integralsätze). Ist auf X zusätzlich eine Metrik g gegeben, so erhält man ein ausgezeichnetes Volumenelement e und einen Hodge-Stern*. Metrik und äussere Ableitung definieren den Gradienten. Die Koableitung einer p-Form f ist die (p - 1)-Form

df: = ( - 1)^{n(p + 1) + s}* d *f,

wobei s die Signatur der Metrik ist. Die Metrik ordnet einem Vektorfeld  v  die 1-Form  zu; die Koableitung von  ist die Divergenz des Vektorfeldes  v . Der Laplace-Beltrami-Operator ist

D = dd + dd.

Im euklidischen   ⁿ (Metrik g_ij = d_ij, s = 0) gilt

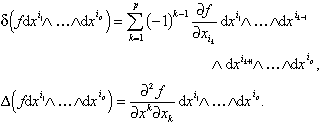
Wichtig ist schliesslich noch der Pullback von Differentialformen (Tensorfelder): Ist f: X  Y eine glatte Abbildung und f Π E (Y), so ist der Pullback f *f eine p-Form auf X, definiert durch

(f *f)_x( v ₁, ...,  v _p) : = f_f(x)(T_x f( v ₁),...,T_x f( v _p))

für Tangentenvektoren  v _i Î T_x(X), wobei T_x f die Ableitung von f an der Stelle x ist (Tangentialraum).

Beispiele: In der Mechanik verwendet man die kanonischen Formen q = p_idqⁱ und w =  - dq = dqⁱ Ù dp_i und das Liouville-Mass W = dq¹ Ù ... Ù dqⁿ Ù dp₁ Ù ... Ù dp_n auf dem Phasenraum. In der Elektrodynamik bilden der Vierer-Strom J = J_mdx^m und das Vierer-Potential A = A_mdx^m 1-Formen. Der Feldstärketensor ist die 2-Form . Damit lauten die Maxwell-Gleichungen: dF = 0 und dF = J. Die Eichfelder A der Yang-Mills-Theorien sind 1-Formen, ihre Feldstärken F sind 2-Formen. In der Thermodynamik bildet man aus der Temperatur T und der Entropie S die 1-Form TdS; das Integral  ò _gTdS über einen Weg (Prozess) g im Phasenraum ist die dem System während des Prozesses insgesamt zugeführte Wärme. In der Allgemeinen Relativitätstheorie können Krümmung und Torsion als 2-Formen interpretiert werden. [SD]