Techniklexikon

Trägheitstensor

Schwingungen und Wellen, tensorielles Trägheitsmoment, ein symmetrischer Tensor zweiter Stufe, mit dem die Trägheitsmomente eines starren Körpers um beliebige Achsen berechnet werden können. Die Komponenten  des Trägheitstensors sind durch

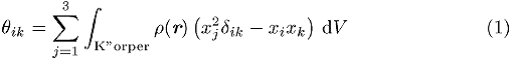
gegeben, wobei  die Massendichte bezeichnet. r ist dabei ein Ortsvektor, der vom Schwerpunkt des starren Körpers aus zu bilden ist. Er sei in einem Koordinatensystem K definiert. Bezüglich einer Achse, deren Richtung durch den Einheitsvektor a gegeben ist und die durch den Schwerpunkt verläuft, erhält man daraus das Trägheitsmoment bezüglich dieser Achse mittels

Dem Trägheitstensor lässt sich, wie jedem symmetrischen Tensor, eine charakteristische Fläche zuordnen, die in diesem Fall als Trägheitsellipsoid bezeichnet wird. Es ist definiert durch die Gleichung

Durch eine entsprechende Wahl des Koordinatensystems K kann der Trägheitstensor auf Diagonalgestalt gebracht werden. In diesem Fall stimmen die Hauptachsen des Trägheitsellipsoids mit den Achsen von K überein und heissen deshalb Hauptträgheitsachsen. Die zugehörigen Diagonalelemente von q werden dann entsprechend als Hauptträgheitsmomente bezeichnet, da sie nach (1) und (2) gerade die Trägheitsmomente bezüglich der Hauptträgheitsachsen sind.

Liegt der Ursprung des Koordinatensystems K nicht im Schwerpunkt des starren Körpers, so gilt der Satz von Steiner, d.h. die Komponenten des Trägheitstensors müssen wie folgt umdefiniert werden, damit (2) seine Gültigkeit behält:

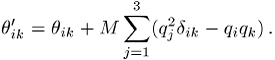
Dabei ist  der Ortsvektor des Schwerpunktes in K und M die Masse des starren Körpers.

Mit Hilfe des Trägheitstensors lassen sich der Drehimpuls L und die Rotationsenergie E eines starren Körpers in übersichtlicher Form angeben. Es gilt  und .