Techniklexikon

Trägheitsmoment

Bezeichnung für die »Drehmasse« eines starren Körpers, die bei dessen Drehung in Erscheinung tritt und der Masse eines sich geradlinig bewegenden Körpers entspricht. Das Tr. entspricht der Summe aller Massenelemente, multipliziert mit dem Quadrat ihrer Abstände zur Drehachse. Ist das Tr. in Bezug auf eine durch den Schwerpunkt des Körpers gehende Achse bekannt, kann das Tr. mit Hilfe des »Steinerschen Satzes« für jede beliebige Achse berechnet werden. Bei der statischen (Mechanik) Berechnung von Baukörpern spielt das sog. Flächentr. eine bedeutende Rolle, bei dem statt eines Körpers nur die Querschnittsfläche, z. B. eines Trägers, betrachtet wird. Für gängige Profilquerschnitte (Profil) sind dieTr. inTabellen festgehalten. Klassische Mechanik, , für einen Massenpunkt mit Abstandsvektor r vom Rotationszentrum über die Gleichung  definierte Grösse. Für ein Vielteilchensystem (z.B. starrer Körper) geht diese Gleichung bezüglich einer vorgegebenen Drehachse in die Summe der mit dem Quadrat  ihres jeweiligen senkrechten Abstands zur Drehachse multiplizierten Masseelemente Dm_i des Körpers über (siehe Abb. 1):

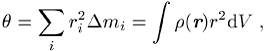
wobei r(r) die Massendichte des Körpers und das Integral über das vom Körper eingenommene Volumen zu bilden ist. Mit der Einführung des Trägheitsmoments kann bei gleichförmiger Rotation des Körpers um eine feste Achse seine kinetische Energie  in Analogie zur gleichförmigen Translation  geschrieben werden; der Masse M des starren Körpers entspricht das Trägheitsmoment , der Geschwindigkeit v die Winkelgeschwindigkeit w.

Rollen also zwei gleich geformte Körper gleicher Masse, aber unterschiedlichen Trägheitsmoments – z.B. ein Vollzylinder aus Holz und ein Hohlzylinder aus Metall – eine schiefe Ebene hinunter, so sind auch deren Winkelgeschwindigkeiten unterschiedlich, d.h. sie rollen unterschiedlich schnell, da wegen der gleichen Massen auf beide das gleiche Drehmoment wirkt (siehe Abb. 2). Auf Grund dieser Analogie wurde das Trägheitsmoment auch als Drehmasse bezeichnet.

Für die Beziehung zwischen Trägheitsmomenten um parallele Achsen gilt der Satz von Steiner. Bei einfacher geometrischer Gestalt des Körpers und homogener Massedichte kann  gewöhnlich einfach berechnet werden; allgemein muss das Trägheitsmoment experimentell bestimmt werden, wozu man entweder Torsionsschwingungen um eine durch den Schwerpunkt gehende Achse oder die (gemessene) Schwingungsdauer (Periode) des physikalischen Pendels zur Hilfe nehmen kann. Die Trägheitsmomente verschiedener homogener Körper zeigt Abb. 3.

Ganz analog zum (Körper-)Trägheitsmoment ist das Flächenträgheitsmoment definiert. Bei einer allgemeinen Drehbewegung reicht die Charakterisierung eines Körpers durch ein Trägheitsmoment nicht aus, es müssen alle durch den Schwerpunkt gehenden Achsen bekannt sein. Daraus ergibt sich das Trägheitsellipsoid (Trägheitstensor). Die Trägheitsmomente in Richtung der Hauptträgheitsachsen heissen Hauptträgheitsmomente, die Achsen mit grösstem bzw. kleinstem (Haupt-) Trägheitsmoment sind freie Achsen, da eine Rotation um diese Achsen auch ohne äussere Fixierung der Achsen stabil bleibt.

Beispiele aus der Praxis: 1) Schwungräder zur Speicherung von Drehenergie in Antriebsmotoren werden mit einem hohem Trägheitsmoment gebaut, um plötzlich auftretenden Widerständen in der Drehbewegung eine hohe Trägheit entgegenzusetzen. 2) Ein Eiskunstläufer beschleunigt die Umdrehungsgeschwindigkeit seiner Pirouette, indem er seine Arme an den Körper zieht: bei erhaltenem Drehimpuls wächst nach  die Winkelgeschwindigkeit im gleichen Masse an, wie das Trägheitsmoment abnimmt (siehe Abb. 4).

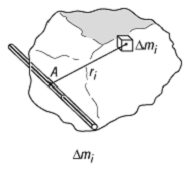
Trägheitsmoment 1: Das Gesamtträgheitsmoment des Körpers als Vielteilchensystem um die Achse A setzt sich zusammen aus der Summe über alle Massenelemente Dm_i multipliziert mit dem jeweiligen Abstand r_i zur Drehachse.

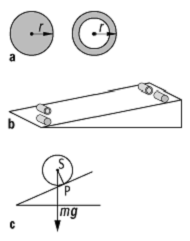
Trägheitsmoment 2: Ein Vollzylinder aus Holz und ein Hohlzylinder aus Metall mit gleichem Radius und gleicher Masse m (a) rollen eine schiefe Ebene hinunter (b). Da auf beide dasselbe Drehmoment wirkt (c), rollt der Körper mit dem kleineren Trägheitsmoment (Vollzylinder) schneller, da er eine grössere Winkelbeschleunigung besitzt.

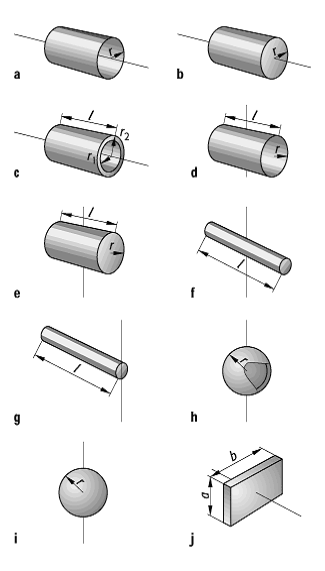
Trägheitsmoment 3: Trägheitsmomente verschiedener homogener Körper der Masse m bezüglich verschiedener Drehachsen. a) Zylindermantel, Drehachse = Körperachse, ; b) Vollzylinder, Drehachse = Körperachse, ; c) Hohlzylinder, Drehachse = Körperachse, ; d) Zylindermantel, Drehachse durch Mittelpunkt senkrecht zur Körperachse, ; e) Vollzylinder, Drehachse durch Mittelpunkt senkrecht zur Körperachse, ; f) dünner Stab, Drehachse durch Mittelpunkt senkrecht zur Körperachse, ; g) dünner Stab, Drehachse durch ein Ende senkrecht zur Körperachse, ; h) dünne Kugelschale, Drehachse durch Mittelpunkt, ; i) massive Kugel, Drehachse durch Mittelpunkt, ; j) massiver Quader, Drehachse durch Mittelpunkt senkrecht zur Oberfläche, .

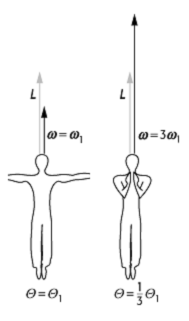
Trägheitsmoment 4: Erhöhung der Winkelgeschwindigkeit bei einer Pirouette durch Erniedrigung des Trägheitsmoments beim Heranziehen der Arme.