Techniklexikon

Dipolfeld

Elektrodynamik und Elektrotechnik, das von einem Dipol, also einer Quellenverteilung mit endlichem Dipol-, aber verschwindendem Monopolmoment, ausgehende Feld (Multipolentwicklung). Für das Feld E_Dipol eines idealen elektrischen Dipols gilt:

(p: elektrisches Dipolmoment, e_r: Einheitsvektor in Ortsvektorrichtung, d(r): d-Funktion, r: Ortsvektor, e₀: Dielektrizitätskonstante des Vakuums). In Polarkoordinaten für einen längs der z-Achse orientieren Dipol mit Mittelpunkt im Ursprung schreibt sich dies als:

,,.

In grossen Entfernungen vom Ursprung verhält sich das Dipolfeld also wie 1/r³ (Fernfeld).

Das Feld eines idealen Dipols ist in der Natur nicht realisiert, da sich dann die Quellen in infinitesimalem Anstand voneinander befinden müssten, während ihre Ladungen gegen  ±  ¥  gingen, wobei das Dipolmoment  unverändert bleiben müsste. Bei einem realen Dipol, z.B. einem Paar elektrischer Punktladungen gleichen Betrags, aber entgegengesetzten Vorzeichens (elektrischer Dipol), oder einem Ringstrom (magnetischer Dipol), gilt die 1/r³-Abhängigkeit nur in hinreichend grossem Abstand vom Dipol. In der Nähe des Ursprungs ist die Feldverteilung wesentlich komplizierter, da hier auch höhere Multipolmomente nicht mehr vernachlässigt werden können (Nahfeld).

                         

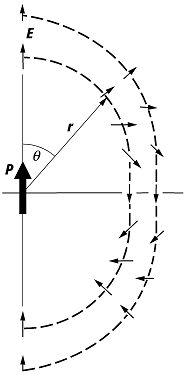
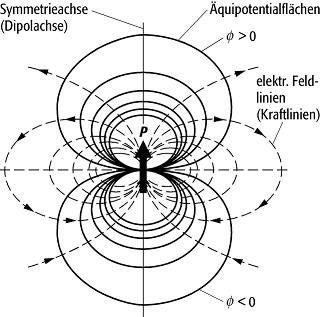
 Dipolfeld: Links: Feld eines elektrischen Dipols. Die Feldstärken sind in einigen Raumpunkten als Pfeile gezeigt, deren Länge proportional zu 1/r³ abnimmt; rechts: Bild der Feldlinien und Äquipotentialflächen. Die Potentialflächen sind rotationssymmetrisch um die p-Achse. Das Potential wird  +  ¥  am Ort des positiven und  -  ¥  am Ort des negativen Ladungsschwerpunkts.