Techniklexikon

Feynman-Integrale

Mathematische Methoden und Computereinsatz^[n], Integrale zur Berechnung von Strahlungskorrekturen bei der Auswertung von Feynman-Diagrammen; sie sind über die inneren Schleifenimpulse dieser Diagramme auszuführen und sind in vielen Fällen divergent, z.B. durch singuläres Verhalten, wenn der Schleifenimpuls sehr gross wird. Beispiel: zum Photonpropagator in der Quantenelektrodynamik trägt in niedrigster Störungsordnung eine Elektronschleife, die sog. Selbstenergie, bei (Abb.). Sie führt auf das Integral

mit der Konvention , wobei p der Schleifenimpuls ist und die Terme innerhalb der eckigen Klammern von den beiden Elektronlinien und ihren Vertizes stammen. Die Photon-Selbstenergie ist auf den ersten Blick quadratisch, tatsächlich aber nur logarithmisch divergent, wie die Rechnung zeigt. Diese lässt sich, genau wie bei anderen divergenten Diagrammen, durchführen, wenn das Integral als vierdimensionaler Grenzfall einer in d ¹ 4 Raumzeit-Dimensionen definierten Funktion betrachtet und somit dimensional regularisiert wird. Alle weiteren mathematischen Operationen wie die Summation über Lorentz-Indizes und die Berechnung des Integrals werden dann in d Dimensionen ausgeführt. Die Resultate werden anschliessend wieder in vier Dimensionen überführt und als Entwicklung in der Variablen e = 4 - d ausgedrückt. Die Divergenzen erscheinen nun als Pole in e, z.B. 1 / e für die logarithmisch divergente Photon-Selbstenergie.

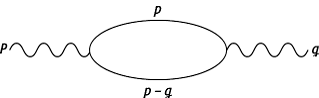
Feynman-Integrale: Selbstenergiediagramm des Photonpropagators, der die Divergenz des entsprechenden Feynman-Integrals bewirkt.