Techniklexikon

fraktale Funktionen

Nichtlineare Dynamik, Chaos, Fraktale, Funktionen mit sehr irregulärem Verhalten (Fraktale). Sie können deterministisch sein, wie die Weierstrass-Mandelbrot-Funktion (Abb.)

 

mit fraktaler Dimension 1 < D < 2, oder stochastischen Ursprungs, wie die Graphen der eindimensionalen Brownschen und der fraktionalen Brownschen Bewegung. Der Exponent 2 - D wird auch als Rauhigkeits- oder Hurst-Exponent bezeichnet. Zeitreihen, die sich durch langreichweitige Korrelationen auszeichnen, führen häufig zu fraktalen Funktionen. Mit Hilfe eindimensionaler fraktaler Funktionen können höherdimensionale Versionen erzeugt werden.

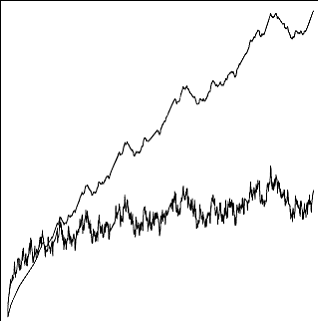
fraktale Funktionen: Die Weierstrass-Mandelbrot-Funktion ist stetig und nirgends differenzierbar. Beispiele mit fraktalen Dimensionen D = 1,3 (glatter) und D = 1,8 (rauher) sind dargestellt.