Techniklexikon

Pauli-Lubanski-Vektor

Quantenmechanik, der im Zusammenhang mit der Poincaré-Gruppe eingeführte Pseudovektor

,

wobei  und  die Poincaré-Algebra erzeugen. Sein Quadrat  ist neben  der zweite Casimir-Operator der Poincaré-Gruppe. Im Ruhesystem eines massiven Teilchens (vektor.gif" alt="Pauli-Lubanski-Vektor">) hat der Pauli-Lubanski-Vektor die Form

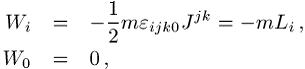
wobei L_i die übliche Drehmatrix in drei Dimensionen ist. Im Ruhesystem ist der Pauli-Lubanski-Vektor also gerade die Erzeugende des Spins. Sein Quadrat ergibt den Spin des Teilchens: . Es ist bemerkenswert, dass alle irreduziblen Darstellung der Poincaré-Gruppe mit den Eigenwerten von  und vektor.gif" alt="Pauli-Lubanski-Vektor"> charakterisiert werden können.