Techniklexikon

Poincaré-Gruppe

Relativitätstheorie und Gravitation, inhomogene Lorentz-Gruppe, zehn-parametrige Gruppe, die sowohl die Rotationen (drei Parameter für die drei Drehachsen) und die zeitlichen und räumlichen Translationen (vier Parameter) als auch die Lorentz-Transformationen (drei Parameter für die drei Raumachsen) enthält. Die Poincaré-Gruppe beschreibt alle im Rahmen der relativistischen Mechanik möglichen Transformationen.

Eine allgemeine Poincaré-Transformation lautet also gruppe.gif" alt="Poincaré-Gruppe">, wobei  ein Element der Lorentz-Gruppe und gruppe.gif" alt="Poincaré-Gruppe"> ein Vierervektor in der Minkowski-Raumzeit ist. Zwei hintereinander geschaltete Poincaré-Transformationen sind durch  definiert, und das Inverse eines Elementes der Poincaré-Gruppe lautet .

Die Erzeugenden  (Lorentz-Generatoren) und  (Translationsgeneratoren) erfüllen die Vertauschungsrelationen

und

Die Casimir-Operatoren lauten  und  mit . Es gilt

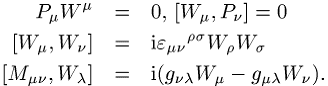
Die unitären irreduziblen Darstellungen der eigentlichen Poincaré-Gruppe () zerfallen in drei Klassen:

1) : die Darstellungen werden durch eine positive Zahl m (Masse) und eine halbzahlige nicht-negative Zahl s (Spin) charakterisiert. Diese Darstellungen beschreiben physikalische massive Teilchen.

2) : dies sind Darstellungen mit imaginärer Masse; sie entsprechen den irreduziblen Darstellungen der dreidimensionalen Lorentz-Gruppe.

3)  (gruppe.gif" alt="Poincaré-Gruppe">): die unitären irreduziblen Darstellungen sind durch  charakterisiert sowie im Fall  durch eine beliebige halbzahlige Grösse h (Helizität) bzw. im Fall  durch ein kontinuierliches Spektrum entsprechend den Darstellungen der dreidimensionalen euklidischen Gruppe E(2). Diese Darstellungen beschreiben physikalische masselose Teilchen.