Techniklexikon

Planetenbewegung

Klassische Mechanik, die Gesetzmässigkeit der Bahnkurve, die die Planeten um die Sonne beschreiben und die aus dem Gravitationsgesetz folgt. Bei der Berechnung der Planetenbahnen kann man sich in erster Näherung auf das Zweikörperproblem Sonne-Planet beschränken. Der Planet steht unter dem Einfluss der Zentralkraft , wobei M die Masse der Sonne,  die des Planeten, r ihr gegenseitiger Abstand und G die Gravitationskonstante bedeuten. In einem Zentralfeld gilt der Drehimpulssatz  Ortsvektor r und Bahngeschwindigkeit v des Planeten bleiben also stets in einer raumfesten Ebene, der Bahnebene, und der Betrag ihres Kreuzproduktes, , ist das Doppelte der vom Radiusvektor in einer Zeiteinheit überstrichenen Fläche (siehe Abb. 1). Aus der Drehimpulserhaltung folgt damit das zweite der Keplerschen Gesetze, der Flächensatz. Aus dem Energie- und Drehimpulssatz kann man weiterhin die Bahngleichung des Planeten ableiten. Es zeigt sich, dass die Bahnformen Kegelschnitten entsprechen. Aus dem Verhältnis von kinetischer zu potentieller Energie kann man folgern, um welchen Bahntyp es sich handelt (siehe Abb. 2). Die Gesamtenergie des Planeten beträgt

Auf einer Kreisbahn ist die Zentrifugalkraft gleich der Anziehungskraft der beiden Massen, also

Beim Anwachsen der kinetischen Energie ergeben sich elliptische Bahnen. Auf der nichtperiodischen Parabelbahn sind im Unendlichen kinetische und potentielle Energie Null. Aus dem Energiesatz folgt dann sofort . Offensichtlich ist ein Körper mit so hoher kinetischer Energie gerade eben nicht mehr ans Zentralgestirn gebunden. Wächst die kinetische Energie noch weiter, so ergeben sich Hyperbelbahnen, die z.B. von nichtwiederkehrenden Kometen beschrieben werden.

Der Einfluss der anderen Planeten auf die Bewegung wird durch Störungsrechnung berücksichtigt. Diese gelangte im 19. Jahrhundert zu solcher Blüte, dass der Ort zweier Planeten aus den Unregelmässigkeiten der Uranusbahn vorhergesagt wurde (Neptun 1846 und Pluto 1930). Die Bewegungsgleichungen eines Planeten lässt sich in der Allgemeinen Relativitätstheorie nicht mehr geschlossen lösen. In erster Näherung ergibt sich die Kepler-Bewegung der klassischen Mechanik, in zweiter Näherung folgt die Perihelbewegung, die Drehung der grossen Halbachse der Ellipsenbahn.

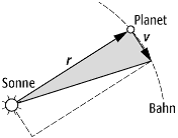
Planetenbewegung 1: Ortsvektor r und Bahngeschwindigkeit v eines Planeten befinden sich stets in einer Ebene.

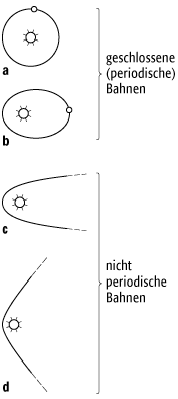
Planetenbewegung 2: a) Kreisbahn E_kin = -E_pot, b) Ellipsenbahn E_pot < E_kin < -E_pot, c) Parabelbahn E_kin = -E_pot, d) Hyperbelbahn E_kin > -E_pot.