Techniklexikon

Riemannsche Geometrie

Relativitätstheorie und Gravitation, Riemannscher Raum, Riemannsche Mannigfaltigkeit, ist eine n-dimensionale, differenzierbare Mannigfaltigkeit, auf welcher ein zweistufig-kovariantes, symmetrisches und nicht entartetes Tensorfeld , genannt Metrik, definiert ist. Dies bedeutet  für beliebige Vektoren  und  sowie  für alle Vektoren , nur wenn  ist. Wählt man nun in dieser Mannigfaltigkeit Koordinaten  und wendet die Metrik auf die infinitesimalen Ortsvektoren  an, so ergibt sich folgende Koordinatendarstellung der Metrik:

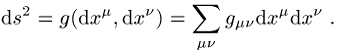
 heisst der Abstand zweier infinitesimal benachbarter Punkte der Riemannschen Mannigfaltigkeit mit der Koordinatendifferenz . Aus obigen Eigenschaften folgt für die Komponenten  der Metrik:

Daraus folgt die Existenz einer inversen Metrik, die ebenfalls symmetrisch ist.

Für einen gegebenen, beliebigen Punkt auf einer Riemannschen Mannigfaltigkeit lassen sich stets Koordinaten dergestalt finden, dass die Metrik diagonal ist und ihre Diagonalelemente nur die Werte  annehmen. Die Zahl der Elemente mit  und derjenigen mit  ist unabhängig von der gewählten Orthonormalbasis und wird als Signatur bezeichnet. Ist die Signatur gleich , so heisst die Metrik riemannsch, ist sie gleich , so heisst sie lorentzsch. Es erhebt sich die Frage, ob man auf einer Riemannschen Mannigfaltigkeit Koordinaten wählen kann dergestalt, dass die Metrik an jedem Punkt Diagonalgestalt (mit Werten ) annimmt. Ist dies der Fall, so heisst die Riemannsche Mannigfaltigkeit flach, sonst gekrümmt. G.F.B. Riemann hat diese Problematik analysiert und einen Tensorkalkül entwickelt, welcher die Beantwortung dieser Frage erlaubt. Aus den Komponenten der Metrik lässt sich ein vierstufiger Krümmungstensor konstruieren, der genau dann überall verschwindet, wenn die Riemannsche Mannigfaltigkeit flach ist.

Durch die Metrik erhält eine Riemannsche Mannigfaltigkeit also eine geometrische Struktur. Insbesondere lassen sich »kürzeste« Verbindungen (Geodäten) zwischen zwei Punkten definieren. Die derartige Kurven beschreibende Gleichung führt zum Konzept des Riemannschen Zusammenhangs.