Techniklexikon

Tschebyschew-Polynome

Mathematische Methoden und Computereinsatz, die Polynome

Sie lassen sich mit Hilfe der Rekursion  und

erzeugen und genügen der Orthogonalitätsbedingung

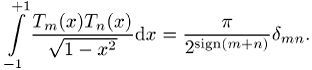
Die Tschebyschew-Polynome besitzen im Intervall   getrennte Nullstellen

Die Tschebyschew-Polynome und in diesem Zusammenhang Tschebyschew-Entwicklungen finden Anwendung bei der numerischen Auswertung von Integralen  auf endlichen Intervallen, bei denen  oszillatorisches Verhalten zeigt. Im Zusammenhang mit der Gauss-Quadratur treten sie mit der Gewichtsfunktion  auf.