Van-Hove-Singularitäten

Petra Nordinghaus-Martin
Festkörperphysik, Singularitäten in der Zustandsdichte g(w) von Normalschwingungen eines Gitters (Phononenzustandsdichte) oder von Elektronen in einem periodischen Kristallpotential.
Van-Hove-Singularitäten sind durch das Verschwinden der
Gruppengeschwindigkeit ![]() charakterisiert. Die Zustandsdichte g(w) steht mit der Dispersionsrelation wj(k) des j-ten phononischen
Zweiges bzw. des elektronischen Bandes mit Bandindex j
durch
charakterisiert. Die Zustandsdichte g(w) steht mit der Dispersionsrelation wj(k) des j-ten phononischen
Zweiges bzw. des elektronischen Bandes mit Bandindex j
durch
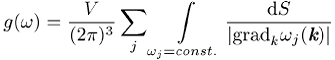
in Beziehung. Verschwindet nun der Gradient gradk w(k) an einem kritischen Punkt wc, so bleibt dort zwar D(w) in dreidimensionalen Gittern stetig, die Ableitung dg(w) / dw jedoch nicht.
Man unterscheidet prinzipiell vier Arten von Van-Hove Singularitäten (siehe Abb.): Mimima, 2 Typen von Sattelpunkten und Maxima. Das Spektrum der Phononenzustandsdichte wird durch das Van-Hove-Theorem beschrieben.
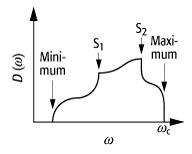
Van-Hove-Singularitäten: Verschiedene Typen von Van-Hove-Singularitäten: Minimum, zwei verschiedene Sattelpunkte und Maximum.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.