Techniklexikon

verschränkte Zustände

Quantenmechanik, Quantenzustände eines zusammengesetzten Systems, die sich nicht als Produkt von Quantenzuständen der Subsysteme ausdrücken lassen, bei zwei Subsystemen also . Die Existenz verschränkter Zustände ist der Hauptunterschied der Quantentheorie gegenüber der klassischen Physik und bringt deren nichtlokalen Charakter (Nichtlokalität) zum Ausdruck. Zustände, welche die mittels einer Lokalitätsannahme abgeleiteten Bellschen Ungleichungen verletzen, sind immer verschränkt. Der Übergang von einem faktorisierenden zu einem verschränkten Zustand ist auch ein wesentlicher Aspekt der Dekohärenz (Kohärenz).

Das prominenteste Beispiel für einen verschränkten Zustand ist der EPR-Zustand

bei dem es sich um einen maximal verschränkten Zustand zweier Spin-1 / 2-Teilchen (Indizes: 1, 2) handelt (EPR-Paradoxon). Ein anderes bekanntes Beispiel für einen verschränkten Zustand ist Schrödingers Katze, deren Analogon für mesoskopische Systeme man in der Quantenoptik experimentell realisieren kann. Das Studium verschränkter Zustände ist insbesondere in dem modernen Gebiet der Quanteninformatik von Bedeutung, da beispielsweise Quantencomputer darauf beruhen, Verschränkungen von Qubits manipulieren zu können.

Ein zweckmässiges Mass zur Beschreibung von Verschränkung ist die Schmidt-Zerlegung: Unterteilt man ein Gesamtsystem in zwei Subsysteme, so kann ein allgemeiner reiner Zustand immer als Einfachsumme geschrieben werden,

wobei  und  jeweils eine (im allgemeinen zeitabhängige) Orthonormalbasis für die Subsysteme bezeichnen. Die lokalen Dichtematrizen, die durch Spurbildung (Spur) über das jeweils andere System entstehen, können dann wie folgt durch Schmidt-Zustände ausgedrückt werden:

und

Unabhängig von der Dimension des Hilbert-Raumes haben die Dichtematrizen die gleichen Eigenwerte, weshalb die lokalen Entropien übereinstimmen. Nützliche Verschränkungsmasse sind die Von-Neumann-Entropie

oder die lineare Entropie

die für einen reinen Zustand verschwinden, weshalb einem faktorisierenden Zustand keine lokale Entropie zukommt.

Wichtig sind auch Verschränkungsmasse, die angeben, wie schnell ein anfänglich faktorisierender Zustand durch eine Wechselwirkung verschränkt wird, was insbesondere bei dem Studium der Dekohärenz eine Rolle spielt. Wenn der Gesamtzustand für  ein Produktzustand von der Form  ist, so hat die Schmidt-Zerlegung nur eine Komponente,  und , weshalb alle Entropien verschwinden. Bilden sich Verschränkungen, so ist (in niedrigster Ordnung in ) . Der Koeffizient  gibt an, wie schnell die beiden Systeme verschränken (»Verschränkungsrate«). Für einen Hamilton-Operator  lautet er

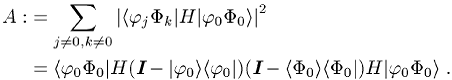
Falls sich die Wechselwirkung  als Produkt zweier Operatoren in den jeweiligen Teilräumen schreiben lässt,

so ist  einfach das Produkt zweier Beiträge, , wobei jeder Faktor durch die Varianz des Anfangszustandes bezüglich der Wechselwirkungsoperatoren gegeben ist,

(und analog für ). Alternativ zu  kann man die Zeitabhängigkeiten der lokalen Entropien betrachten.