Techniklexikon

Yang-Baxter-Gleichungen

Thermodynamik und statistische Physik, algebraische Relationen, die im Zusammenhang mit zweidimensionalen integrablen Modellen der Physik gefunden wurden. Mathematisch handelt es sich um Gleichungen zwischen linearen Abbildungen auf Tensorprodukten von Vektorräumen, die beispielsweise für die Darstellungstheorie von Hopf-Algebren und Quantengruppen relevant sind. Physikalisch kann es sich um Relationen zwischen Elementen einer Streumatrix (S-Matrix, C.N. Yang, 1967) oder zwischen Boltzmann-Faktoren in Gittermodellen (R.J. Baxter, 1972) handeln (siehe Abb.). Die Yang-Baxter-Gleichungen treten auch in der topologischen Quantenfeldtheorie, in zweidimensionalen konformen Feldtheorien oder in der Knotentheorie auf. In der älteren Literatur findet man oft die Bezeichnung Star-Triangle-Relationen.

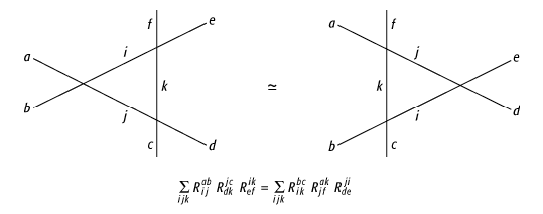
Yang-Baxter-Gleichung: Graphische Darstellung. Gezeigt ist ein Ausschnitt eines (irregulären) Gitters, auf dem ein Vertex-Modell mit Zuständen  auf den Gitterlinien definiert ist.  seien die Boltzmann-Faktoren an den Vertizes. Die Zustandssummen für die beiden Gitterarten sind gleich, wenn die Boltzmann-Faktoren die Yang-Baxter-Gleichung erfüllen.