Techniklexikon

Quantenfeldtheorie

Teilchenphysik^[n], QFT, relativistische Quantentheorie zur Beschreibung der Elementarteilchen und ihrer Wechselwirkungen, die vom Wellencharakter der Materie ausgeht und den Teilchenaspekt durch die Quantisierung der entsprechenden, relativistisch formulierten, klassischen Feldtheorie einführt. Die Quantenfeldtheorie ist sehr gut bestätigt - in Form der Quantenelektrodynamik mit einzigartiger Präzision - und wird erfolgreich auch ausserhalb der Elementarteilchenphysik angewandt, z.B. bei der Beschreibung der Supraleitung und des Quanten-Hall-Effektes.

Die Basis der Quantenfeldtheorie bilden drei Grundprinzipien: die Identifizierung der dynamischen Freiheitsgrade mit Operatorfunktionen (Feldern), die Lokalität der Wechselwirkungen und die Beachtung fundamentaler Symmetrien (Lorentz-, Eichsymmetrie). Darauf aufbauend erklärt sie (zunächst als freie Theorie) die Existenz von Teilchen als angeregte Zustände der entsprechenden Felder, die Zuordnung einer Statistik zu jeder Klasse von Teilchen (Fermionen, Bosonen) sowie die Existenz von Antiteilchen. Betrachtet man zusätzlich Wechselwirkungen, folgen aus der Quantenfeldtheorie das Konzept der Teilchenerzeugung und -vernichtung und die Assoziation der Wechselwirkungen mit Teilchenaustausch.

Neben diesen allgemeinen, gleichwohl herausragenden Konsequenzen der Quantenfeldtheorie liegt ihre tiefere physikalische Bedeutung in der durch die Lokalität der Wechselwirkung begründete Notwendigkeit, unendlich viele Freiheitsgrade einzuführen: will man das lokale Feld  für einen Raumzeitpunkt  konstruieren, muss man es als Superposition

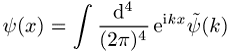
formulieren, wobei die Feldkomponenten  von beliebig grossen Impulsen abhängen können. Vor diesem Hintergrund erweist es sich als nicht-triviale und zusätzliche einschränkende Prozeduren verlangende Aufgabe, konsistente Quantenfeldtheorien zu konstruieren; dies führt direkt zur Theorie der Renormierung und den Konzepten der laufenden Kopplungskonstanten und der asymptotischen Freiheit.

Der Formalismus der Quantenfeldtheorie hat als Ausgangspunkt die Lagrange-Dichten für freie Spin-0-, Spin-1 / 2- und Spin-1-Teilchen,

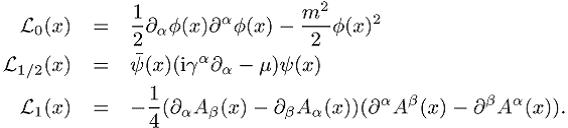
sowie die Verallgemeinerung auf nicht-abelsche Vektorfelder. Die Wechselwirkungen werden durch lokale Produkte der Felder und ihrer Ableitungen sowie einem Koeffizienten, der Kopplungskonstanten, eingeführt, wobei die Kopplung die richtige Dimension besitzen muss, damit die Lagrange-Dichte (in natürlichen Einheiten) insgesamt die Dimension (Masse)⁴ hat. Störungstheoretisch macht es keinen Sinn, Kopplungen mit negativer Dimension zu haben; entsprechende Wechselwirkungen sind nicht renormierbar (Renormierung).

Die übliche Prozedur zur Quantisierung der Felder ist die kanonische Quantisierung, die konjugierte Felder und Vertauschungsrelationen einführt, die sich mit Fourier-Darstellungen der Felder erfüllen lassen, beispielsweise für ein skalares Feld

wobei sich  und  als Erzeugungs- bzw. Vernichtungsoperator identifizieren lassen.

Die aus der Lagrange-Dichte mit wechselwirkenden Feldern abgleiteten Feldgleichungen lassen sich nur störungstheoretisch behandeln, vorausgesetzt, die Kopplungskonstante ist klein. R. Feynman hat ein Verfahren entwickelt, alle Terme der Störungsreihe zu konstruieren und mit einer präzisen Rechenvorschrift zu verknüpfen (Feynman-Diagramm).