Techniklexikon

Quantengruppen

Quantenmechanik, von den russischen Mathematikern Manin und Drinfeld einerseits sowie Fadejew, Reschetikin, Skljanin und Taktajan andererseits in den achtziger Jahren formulierte und untersuchte algebraische Strukturen, die im weitesten Sinne als »Quantisierung von Lie-Gruppen« aufgefasst werden können und mathematisch die Struktur von Hopf-Algebren haben.

Manin geht dabei von einer konkreten Matrixdarstellung der Gruppe aus, beispielsweise der SL(2,C), der komplexen (2 ´ 2)-Matrizen mit Determinante 1,

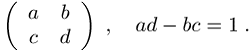
Die komplexen Zahlen a, b, c, d werden nun durch eine nicht-kommutative Algebra ersetzt, wobei Relationen der Form

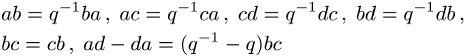
mit einer komplexen Phase q gelten sollen. Die Determinantenbedingung lautet nun . Die so erhaltenen »Matrizen« bilden zwar keine Gruppe im herkömmlichen Sinne mehr, aber viele der ursprünglichen Relationen gelten nach wie vor.

Fadejew et al. betrachten die Lie-Algebra einer Lie-Gruppe und verändern die Produktrelationen zu nicht-kommutativen Produkten, wodurch sich auch die Definition des Kommutators ändert. Als Konsistenzbedingungen für ein assoziatives Produkt treten Gleichungen auf, die den Yang-Baxter-Gleichungen entsprechen. Gefunden wurden die Strukturen der nicht-kommutativen Gruppen im Zusammenhang mit integrablen Modellen, insbesondere der Quanten-Inversen-Streumethode. Heute finden sie unter anderem in der Quantenfeldtheorie und der mathematischen Physik Anwendung.

Die Heisenberg-Algebra in der Physik lässt sich als Quantengruppe zu der zweidimensionalen Translationsgruppe auf dem Phasenraum auffassen. Im Sinne der nicht-kommutativen Geometrie erhält man Quantengruppen auch durch die Ersetzung der kommutativen Funktionenalgebra auf Gruppen durch eine nicht-kommutative Algebra.