Techniklexikon

AB-Kette

ein eindimensionales Kristallmodell. M. Born und Th. von Kármán entwickelten dieses Modell, das von einer unendlich langen linearen Kette ausgeht, in der Atome der Atomsorte A mit der Masse m_A und solche der Sorte B mit der Masse m_B im gleichen Abstand d aufeinanderfolgen. Die Kette besteht also aus Zellen mit dem Basisvektor a = 2d und mit zwei Atomen pro Elementarzelle. Legt man den Koordinatenursprung in die Ruhelage eines A-Atoms, so sind durch x_A = 2nd = na (n = 0, ± 1, ± 2,...) die Ruhelagen aller A-Atome und durch x_B = x_A ± d = (2n ± 1)d = (n ± 1/2)a die Ruhelagen aller B-Atome festgelegt. Im folgenden wird ein lineares Kraftgesetz vorausgesetzt, und es werden nur Longitudinalwellen betrachtet; weiter soll jedes Atom nur Kräfte von seinen nächsten Nachbarn erfahren. Damit ist eine rücktreibende Kraft nur dann wirksam, wenn die Abstände von den beiden Nachbarn rechts und links verschieden gross sind, diese Kraft ist damit proportional zur Abstandsdifferenz. Die Atome können um ihre Ruhelage schwingen, wobei die Auslenkung des i-ten Atoms aus seiner Ruhelage mit u_i bezeichnet werden soll. Für die A-Atome (gerade Indizes) sind also die Abstände vom 2n-ten Atom von seinem Nachbarn rechts und links gegeben durch:

d ₊  = d + u_{2n + 1} - u_2n,

d _-  = d + u_2n - u_{2n - 1}, n = 0, ± 1,...

Die Bewegungsgleichungen der A-Atome lauten somit

,

analog ergibt sich für die B-Atome (ungerade Indizes):

.

Die Federkonstante a ist natürlich für beide Atomsorten die gleiche, da die rücktreibende Kraft durch die wechselseitige Bindung zwischen A- und B-Atomen hervorgerufen wird. Als Lösung der Bewegungsgleichungen ergeben sich harmonische Wellen (Eigenwellen) mit noch zu bestimmenden komplexen Amplituden und der Kreisfrequenz w. Mit dem Wellenvektor k = (k_x,0,0), k = 2p/l = w/ (l: Wellenlänge, : Phasengeschwindigkeit der Wellen), folgt als Bedingungsgleichung die Dispersionsrelation, die den Zusammenhang zwischen Frequenz und Wellenvektor angibt. Deren Lösungen sind die beiden Dispersionszweige

welche periodisch in k a mit der Periode 2p sind. Damit kann man alle erlaubten Eigenwellen konstruieren, wenn man die Wellenzahl auf  - p < k a £ p bzw. den Wellenvektor auf  - g/2 < k £ g/2 beschränkt. Alle Eigenwellen liegen so in der ersten Brillouin-Zone. Deren Breite ist mit  gleich der Länge des Basisvektors der zugehörigen reziproken Kette.

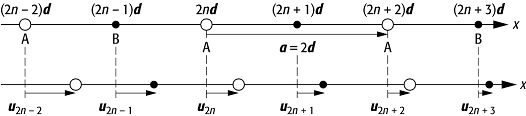
AB-Kette: unendliche AB-Kette, oben in Ruhelage, unten während einer Longitudinalwelle. Offene Kreise (gerade Indizes): A-Atome, volle Kreise (ungerade Indizes): B-Atome.