Techniklexikon

Bayessche Statistik

subjektive Wahrscheinlichkeit, ein Modellansatz bezüglich der Frage, wie experimentelle Ergebnisse unmittelbar für die Theoriebildung verwendet werden können. Die Bayessche Statistik geht auf einen 1763 posthum veröffentlichten Aufsatz des britischen Geistlichen Thomas Bayes (1702-1761) zurück. Grundlage für die Bayessche Statistik ist die Umdeutung der Bayesschen Formel

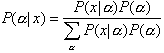
dahingehend, dass die x als mögliche Ausgänge eines Experimentes anzusehen sind, die a dagegen als Hypothesen ("Theorien") darüber, welche Ausgänge x mit welchen Wahrscheinlichkeiten zu erwarten seien. P(a ô x) ist die Wahrscheinlichkeit für die Hypothese a, nachdem man x gemessen hat. P(x ô a) ist die Wahrscheinlichkeit für den Ausgang x des Experimentes unter der Annahme, dass Theorie a richtig ist. Wenn die Theorie in Bezug auf das durchgeführte Experiment aussagekräftig ist, dann sollte sich P(x ô a) berechnen lassen. Die P(a) sind A-priori-Wahrscheinlichkeiten der Theorien a vor Durchführung des Experimentes. Sie beruhen entweder auf reinen Verstandesüberlegungen (z.B. Symmetrieargumenten) oder auf dem bisherigen Stand der Wissenschaft. Das Setzen der A-priori-Wahrscheinlichkeiten ist allerdings auch mit einer gewissen Willkür verbunden. Für die Bayessche Statistik gilt die folgende Variante des zentralen Grenzwertsatzes: Werden die Theorien durch einen Parameter a charakterisiert, dessen wahrer Wert a₀ ist, dann geht p(a ô x₁,...,x_N) - das ist die aus N Messungen ermittelte Wahrscheinlichkeitsverteilung für den Parameter a - für grosse N gegen eine Gauss-Verteilung mit Mittelwert a₀, deren Varianz wie 1/N abnimmt. Insbesondere verschwindet für grosse N die Abhängigkeit der A-posteriori-Verteilung P(a ô x₁,...,x_N) von der A-priori-Verteilung p(a).