Techniklexikon

chaotische Wellenfunktion

ein Begriff aus dem Gebiet des Quantenchaos, für den es keine allgemein akzeptierte Definition gibt. Gemeint sind Eigenfunktionen klassisch chaotischer Quantensysteme, die in einer Phasenraumdarstellung wie beispielsweise durch Wigner-Funktionen (oder ihren geglätteten Versionen) überwiegend in chaotischen Komponenten des Phasenraums lokalisiert sind (fast-integrable Systeme, Chaos). Exakt kann dies nur im semiklassischen Limes  erfüllt sein. Trotzdem spricht man auch für  von chaotischen Wellenfunktionen, wenn diese genügend irregulär erscheinen. Als Mass für die Irregularität dienen oft Korrelationsfunktionen der Wahrscheinlichkeitsamplitude der Wellenfunktion, z.B. in der Ortsdarstellung, oder das Verhalten ihrer Knotenlinien (Null-Amplitude). Ein Beispiel hierfür ist die in der Abb. dargestellte Wellenfunktion Y(x, y) für das klassisch völlig chaotische Bunimowitsch-Stadion.

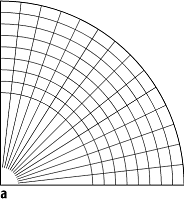
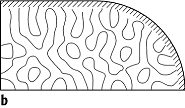
chaotische Wellenfunktion: a) Reguläre Knotenlinien eines klassisch integrablen Systems (Kreisbillard) im Vergleich zu den Knotenlinien des klassisch chaotischen Bunimowitsch-Stadions (b).