Techniklexikon

Ellipse

Klassische Mechanik, ebene geometrische Figur, die zu den Kegelschnitten gehört. In der analytischen Geometrie ist die Ellipse der Ort aller Punkte mit den Koordinaten (x, y), die die Gleichung  erfüllen. a und b heissen die Halbachsen der Ellipse, wobei a vereinbarungsgemäss die längere der beiden ist. Der Kreis ist eine entartete Ellipse mit a = b = r, wobei r den Radius des Kreises darstellt. Zur Charakterisierung der Ellipse werden einige weitere Parameter eingeführt: die lineare Exzentrität e² = a² - b² und die numerische Exzentrität e = e / a < 1. Diese letzte Eigenschaft ist charakteristisch für die Ellipse, für die Hyperbel gilt e > 1, für die Parabel ist e = 1. Die Brennpunkte der Ellipse auf der langen Achse werden durch die sogenannte erste Fundamentaleigenschaft definiert: Bildet man ein Dreieck mit der Strecke zwischen ihnen als einer Seite und einem beliebigen Punkt der Ellipse als drittem Punkt, so ist der Umfang aller dieser Dreiecke gleich.

Die Ellipse ist die Form gebundener Bahnen im Gravitationsfeld bei Gültigkeit der Newtonschen Gesetze. Dabei ist einer der Brennpunkte der Ellipse das Zentrum der Bewegung, um das die Schwerpunkte der gravitierenden Körper rotieren. Bei sehr grossem Massenunterschied der beiden Körper (z.B. Sonne-Planet oder Erde-Satellit) kann angenommen werden, dass der Zentralkörper in einem der Brennpunkte ruht. Bei der Planetenbewegung heissen die beiden Endpunkte der langen Hauptachse, also der sonnennächste und fernste Punkt, Perihel und Aphel.

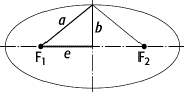
Ellipse: Die charakterisierenden Parameter einer Ellipse.