Energiefläche

Hermann Loring
FestkörperphysikNichtlineare
Dynamik, Chaos, Fraktale, 1) Mechanik: die Fläche H(q, p) = E konstanter Energie E im
Phasenraum eines konservativen Hamilton-Systems mit Hamilton-Funktion H(q, p).
Die chaotische oder reguläre Bewegung eines Zustands, beschrieben durch die
Hamiltonschen Bewegungsgleichungen, ist auf eine Energiefläche beschränkt (Energiesatz),
wobei die Anfangswerte
q(t normal;
font-style:normal\'>=normal;font-style:normal\'> 0), p(t normal;font-style:normal\'>=normal;font-style:normal\'> 0) von Koordinate
und konjugiertem Impus die Energie E festlegen. Die
Energiefläche ist typischerweise gekrümmt. Z.B. für einen n-dimensionalen
harmonischen Oszillator ist sie topologisch eine (2n - 1)-dimensionale
Hyperkugelfläche S2n-1.
2) Festkörperphysik: Flächen konstanter Elektronenenergie im k-Raum, deren Form sich aus der Abhängigkeit der Bandenergie e(k) vom Wellenvektor k ergeben. Für kleine k in der Nähe des Zentrums der 1. Brillouin-Zone verschwindet die 1. Ableitung Ñke, so dass in erster Näherung
![]()
gilt (das Koordinatensystem wird so gewählt, dass die gemischten Ableitungen verschwinden) und die Energieflächen e(k) = const. ellipsoidförmig sind. In manchen Fällen sind die effektiven Massen mi*, definiert durch
![]() ,
,
unabhängig von der Richtung von k, und man erhält wegen mi* = mj* kugelförmige Energieflächen. In primitiven kubischen Gittern sind auch in der Umgebung der Eckpunkte der 1. Brillouin-Zone die Flächen konstanter Energie Kugelschalen um die Eckpunkte, wie es in der Abbildung schematisch dargestellt ist. Spezielle Energieflächen sind die Fermi-Flächen.
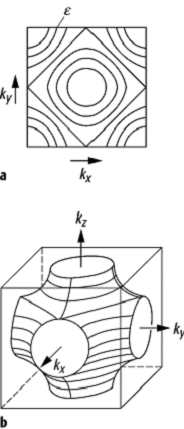
Energiefläche: Kurven konstanter Energie in der kxky-Ebene der 1. Brillouin-Zone eines kubisch primitiven Gitters (a) und eine Energiefläche im k-Raum (b).
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.