Techniklexikon

Hodge-Stern

Mathematische Methoden und Computereinsatz, Hodge-Operator, Isomorphismus * zwischen p-Formen und (n - p)-Formen, der durch eine Metrik g auf einer orientierten n-dimensionalen Mannigfaltigkeit X ausgezeichnet wird (Differentialformen). Ist (e¹, ..., eⁿ) ein positiv orientiertes orthonormales n-Bein zur Metrik g und e = e¹ Ù ... Ù eⁿ das von g und der Orientierung erzeugte Volumenelement, so gilt e = *1, *e = (-)^s,

wobei s = 0 für eine Riemannsche Metrik (det g > 0) und s = 1 für eine pseudo-Riemannsche Metrik (det g < 0). Doppelte Anwendung des Hodge-Sterns auf eine p-Form f liefert wieder eine p-Form: **f = (-)^p(n-p)+s f.

Es gelten die Rechenregeln:

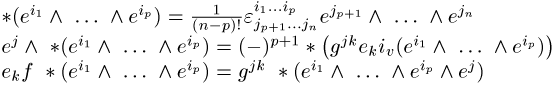
Beispiele: 1) X = ³, g_ij = d_ij. Zur 1-Form B = B_i dxⁱ des magnetischen Feldes gehört die 2-Form *B, deren Integral  über eine Fläche S gleich dem magnetischen Fluss durch S ist.

2) X = ⁴, g_ab = h_ab (Minkowski-Metrik). Der Feldstärketensor F der Elektrodynamik ist eine 2-Form, *F ist der duale Feldstärketensor.