Techniklexikon

Legendresche Differentialgleichung

Spezialfall der zugeordneten Legendresche Differentialgleichung

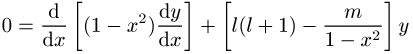
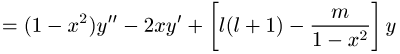
für . Die zugeordnete Legendresche Differentialgleichun entsteht, indem man in der Laplace-Gleichung  den Separationsansatz  mit  verfolgt; dieses Problem stellt sich z.B. in der Elektrostatik. Für  und  sind die Lösungen der zugeordneten Legendreschen Differentialgleichung durch die zugeordenten Legendre-Polynome , für  durch die Legendre-Polynome gegeben. Die Legendresche Differentialgleichung tritt meist auf im Zusammenhang mit der Separation der Variablen bei der Lösung der Laplace-Gleichung in Kugelkoordinaten, z.B. bei der Lösung der Schrödinger-Gleichung des Wasserstoffatoms.