Techniklexikon

Navier-Stokes-Gleichungen

Strömungsmechanik, Gleichungssystem, welches die Dynamik einer viskosen Flüssigkeit (Flüssigkeit, viskose) beschreibt. Für inkompressible Flüssigkeiten (Flüssigkeit, inkompressible) zeitlich und räumlich konstanter Zähigkeit lautet es:

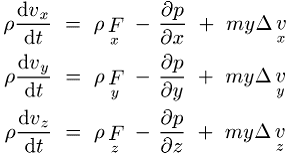
(v_x, v_y, v_z: Geschwindigkeitskomponenten eines Flüssigkeitsteilchens in x, y, oder z-Richtung, d / dt: totale Ableitung nach der Zeit, r: die als konstant angenommene Dichte der Flüssigkeit, F_x, F_y, F_z: Beschleunigungskomponenten der Masseteilchen durch die Massenkraft, p: Druck in der Flüssigkeit und m: die ebenfalls als konstant angenommene dynamische Viskosität).

Die Navier-Stokes-Gleichungen können aus den Eulerschen Gleichungen durch Hinzufügen des Termes, der die Reibungskräfte beschreibt, gewonnen werden. Die Gleichungen bilden die Grundlage der gesamten Hydrodynamik der viskosen Flüssigkeiten. Durch Vernachlässigen der verschiedenen Terme und Abhängigkeiten werden die Gleichungen erhalten, die anwendbar sind auf die speziellen Probleme der Hydrodynamik, welche die Grundlage der einzelnen Teilgebiete bilden.

Die Navier-Stokes-Gleichungen bilden zusammen mit der Kontinuitätsgleichung ein System von vier Differentialgleichungen für die vier Unbekannten v_x, v_y, v_z und p. Die analytische Lösbarkeit ist jedoch nur für Spezialfälle möglich (Couette-Strömung, Hagen-Poiseuillesches Gesetz). Zur allgemeinen Behandlung ist man daher auf numerische Verfahren angewiesen.