Techniklexikon

Newtonsche Ringe

Optik, Newton-Ringe, Interferenzsystem, bestehend aus hellen und dunklen Kreisen um den Berührungspunkt von einer schwach gekrümmten Konvexlinse und einer planen Glasplatte, wenn diese gegeneinander gedrückt werden. Fällt ein monochromatisches Parallelbündel der Wellenlänge l senkrecht bzw. unter einem kleinen Einfallswinkel ein, so beobachtet man sowohl in Reflexion als auch in Durchsicht diese Ringe, die nach seinem Entdecker als Newtonsche Ringe bezeichnet werden. Der Abstand der Ringe nimmt von innen nach aussen hin ab (siehe Abb. 1), da die Dicke der Luftschicht zwischen der Glasplatte und der Linsenfläche nicht proportional zum Abstand des Berührungspunktes ist, sondern rascher ansteigt (siehe Abb. 2). Erst Young konnte dieses Phänomen durch den Begriff der Interferenz vollständig erklären. Ähnliches beobachtet man bei zwei im Winkel a montierten Glasplanflächen mit Parallellicht. Das hier beobachtete Interferenzsystem besteht aus hellen und dunklen Streifen gleicher Dicke, die als Fizeau-Streifen bezeichnet werden. Für ein einfallendes monochromatisches Parallelbündel mit einem Einfallswinkel a ergibt bei einer Luftkeildicke d ein Gangunterschied .

Der zusätzliche Beitrag 1 / 2 rührt daher, dass es in der Luftschicht zu einem Phasensprung am dichteren Medium kommt. Bei senkrechtem Einfall und mit einer Brechzahl n = 1 vereinfacht sich der Ausdruck zu . Ist der Gangunterschied gleich einem ungeradzahligen Vielfachen von l / 2, so kommt es zur Schwächung wie im Zentrum mit d = 0 (destruktive Interferenz). Im anderen Fall kommt es zu einer konstruktiven Interferenz. Der Abstand zweier benachbarter heller bzw. dunkler Streifen voneinander entspricht demnach einer Änderung des Gangunterschiedes um l. Fällt divergentes Licht auf das System, so ist der Gangunterschied zwischen den Teilwellen zusätzlich vom Einfallswinkel abhängig und die Interferenzen gleicher Neigung werden als Haidinger Ringe bezeichnet.

Mit Hilfe der Newtonsche Ringe kann der Krümmungsradius r einer schwach gekrümmten Konvexlinse exakt bestimmt werden. Betrachtet man zwei Ringe verschiedener Ordnungszahl (m > n) mit d_m = m l / 2 bzw. d_n = n l / 2 und Radius a_m und a_n, so ist der Krümmungsradius bestimmt durch:

.

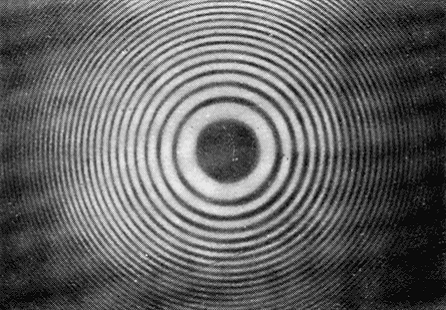
Newtonsche Ringe 1: Newtonsche Ringe inreflektiertem monochromatischen Licht. (aus: Bergmann/Schäfer, Lehrbuch der Experimentalphysik Bd. 3)

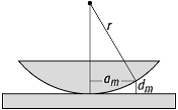
Newtonsche Ringe 2: Anordnung zur Beobachtung mit den relevanten Grössen.