Techniklexikon

Newtonsche Sterne

Relativitätstheorie und Gravitation, Sterne, deren Gravitationsfeld hinreichend schwach ist. Falls

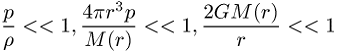
gilt, wobei  die Materiedichte,  der Druck und  die innerhalb einer Kugel mit Radius  enthaltene Materiemenge ist (die Einheiten sind so gewählt, dass  gilt), geht die Oppenheimer-Volkoff-Gleichung über in

Diese Beziehung ist nichts anderes als die nicht-relativistische Gleichgewichtsbedingung zwischen Druckkraft und Gravitationskraft im Stern. Setzt man hierin nun die polytrope Zustandsgleichung  ein und löst die so entstandene Differentialgleichung, so ergeben sich Sternradius  und Sternmasse  als eindeutige Funktion der zentralen Dichte :

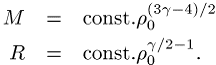
Dabei lassen sich die Konstanten mit Hilfe der Lane-Emden-Funktion zum Index } berechnen.

Durch Untersuchungen von Auslenkungen aus der Gleichgewichtslage erhält man als eine notwendige Bedingung für Stabilität: . Anwendbar ist das Modell des Newtonschen Sternes nicht nur auf sonnenähnliche Sterne (dort erzeugt die Temperaturbewegung einen kinetischen Druck, welcher der Gravitation entgegenwirkt), sondern auch auf Weisse Zwerge und Neutronensterne, sofern die Zentraldichte  nicht zu hoch ist. Man erhält dort  gleich  bzw. .