Padé-Approximation

Hans-Peter Ahlsen
Mathematische
Methoden und Computereinsatz, Approximation einer Funktion ![]() in der ganzen komplexen Ebene mit
Hilfe einer Funktion
in der ganzen komplexen Ebene mit
Hilfe einer Funktion ![]() (Padé-Approximant),
die aus einem Zähler- und Nennerpolynom besteht und sich aus den Koeffizienten
der Taylor-Entwicklung von
(Padé-Approximant),
die aus einem Zähler- und Nennerpolynom besteht und sich aus den Koeffizienten
der Taylor-Entwicklung von ![]() ableitet. Die Potenzreihenentwicklung eines
Padé-Approximanten stimmt überein mit den Koeffizienten einer vorgegebenen
Potenzreihe
ableitet. Die Potenzreihenentwicklung eines
Padé-Approximanten stimmt überein mit den Koeffizienten einer vorgegebenen
Potenzreihe ![]() , d.h.
, d.h.
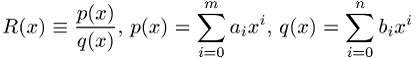
ist genau dann Approximant der Reihe ![]() , wenn gilt
, wenn gilt
![]()
das Monom niedrigster Ordnung des Differenzpolynoms
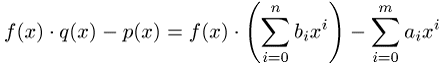
also von der Ordnung ![]() oder höherer Ordnung ist. Diese Bedingung
liefert
oder höherer Ordnung ist. Diese Bedingung
liefert ![]() Gleichungen für
die
Gleichungen für
die ![]() Unbekannten
Unbekannten approximation.gif" alt="Padé-Approximation"> und
![]() , die sich (nach einer Normierung
, die sich (nach einer Normierung approximation.gif" alt="Padé-Approximation">) im Prinzip berechnen
lassen; in der Praxis und aus Stabilitätsgründen werden Padé-Approximanten
jedoch meist mit Hilfe rekursiver Techniken berechnet.
Das Konzept der Padé-Approximation lässt sich auf vektorwertige Funktionen mit vektorwertigem Argument erweitern. Sie spielt eine wichtige Rolle in vielen numerischen Algorithmen (Lösung nichtlinearer Gleichungen, Integration, Differentialgleichungen, Konvergenzbeschleunigung, Approximation spezieller Funktionen), bei der Untersuchung nichtlinearer Probleme oder divergenter Reihen, in der Physik, Chemie, Mechanik, Strömungsmechanik oder der Theorie elektrischer Schaltkreise.
Techniklexikon.net
Das freie Technik-Lexikon. Fundierte Informationen zu allen Fachgebieten der Ingenieurwissenschaften, für Wissenschaftler, Studenten, Praktiker & alle Interessierten. Professionell dargeboten und kostenlos zugängig.
Techniklexikon
Modernes Studium der Physik sollte allen zugängig gemacht werden.