Techniklexikon

periodische Bewegung

Klassische Mechanik, bezeichnet die zeitliche Entwicklung eines mechanischen Systems, bei der bestimmte Werte der Koordinaten und Impulse des Systems immer wieder angenommen werden. Mit anderen Worten bedeutet dies, dass sich die Entwicklung des Systems beständig wiederholt. Ein Beispiel hierfür ist die elastische Schwingung: In jeder Periode der Oszillation wird jeder Bahnpunkt zweimal durchlaufen, mit entgegengestzten, aber betragsgleichen Impulswerten. 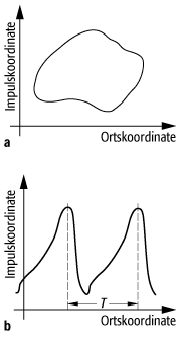Im zweidimensionalen Phasenraum ist die Phasentrajektorie einer Schwingung mit einem Freiheitsgrad eine Ellipse. Man spricht hier auch von einer Librationsbewegung (siehe Abb 1a). Einen zweiten Fall der periodischen Bewegung stellt die Rotationsbewegung dar: während die Impulskoordinate periodisch dieselben Werte annimmt, wächst die Ortskoordinate, hier ein Winkel, kontinuierlich an. Dies scheint jedoch ein Artefakt der Methode, Winkel zu messen, zu sein, denn der mechanische Zustand des Systems ist identisch für die Werte des Winkels  usw. (siehe Abb. 1b). 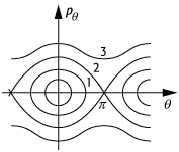Eine Librationsbewegung kann nahtlos in eine Rotation übergehen, beispielsweise beim Pendel: Ist die Energie der Pendelbewegung nicht zu hoch, so führt es eine Schwingung zwischen zwei Grenzwinkeln  aus (Phasentrajektorie 1 in Abb.2), bei Zufügung von Energie geht die Bewegung in eine Rotation über und  kann beliebige Werte annehmen (Phasentrajektorie 3 in Abb. 2).

periodische Bewegung">

periodische Bewegung 1: Bahn eines Systempunktes im Phasenraum: a) Librationsbewegung, b) Rotationsbewegung mit Periode T.

periodische Bewegung">

periodische Bewegung 2: Drei Phasentrajektorien des einfachen Pendels.