Techniklexikon

Determinante

Mathematische Methoden und Computereinsatz, die einer n ´ n-Matrix a_ij zugeordnete Zahl , wobei e_ijk... = 1 ist, wenn die i,j,k... eine gerade Permutation von 1,2,3,... sind, e_ijk... =  - 1 im Falle einer ungeraden Permutation und e_ijk... = 0, wenn sich ein Index wiederholt (Levi-Civita-Symbol). (Eine Permutation heisst gerade, wenn sie sich aus einer geraden Zahl von Transpositionen zusammensetzt.) Man schreibt

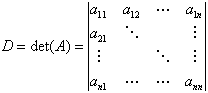
Etwas handlicher ist die rekursive Definition

für beliebige j, die man Laplacesche Entwicklung nach der j-ten Spalte nennt; die Matrix B_ij erhält man, wenn man aus A die i-te Zeile und die j-te Spalte streicht. Für das Rechnen mit Determinanten gelten folgende Regeln: a) det(A^T) = det(A), b) det(kA) = kⁿ det(A), c) det(A + B) = det(A) + det(B), d) Vertauschung zweier Zeilen oder Spalten kehrt das Vorzeichen der Determinante um, e) det(A) = 0, wenn A singulär ist; det(A) ¹ 0 ist äquivalent dazu, dass die inverse Matrix A ^{- 1} existiert, f) det(AB) = det(A)det(B), also insbesondere det(B ^{- 1}AB) = det(A), d.h. ähnliche Matrizen besitzen dieselbe Determinante, g) die Determinante einer Dreiecksmatrix ist gleich dem Produkt der Diagonalelemente.

Die Determinante einer 3 ´ 3-Matrix ist

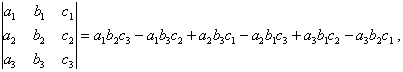
dies ist gleichbedeutend mit dem Spatprodukt . Eine orthogonale 3 ´ 3-Matrix beschreibt genau dann eine Drehung, wenn ihre Determinante  + 1 beträgt, ist sie dagegen -1, handelt es sich um eine Drehspiegelung. Die numerische Lösung eines linearen Gleichungssystems Ax = b gestaltet sich dann besonders schwierig, wenn die Matrix A nahezu singulär, d.h. wenn det(A) << 1 ist.

In quantenmechanischen Systemen aus mehreren Fermionen, z.B. bei Atomen mit mehr als einem Elektron, spielt die Slater-Determinante eine Rolle. Die Determinante der Jacobi-Matrix wird für allgemeine Koordinatentransformationen benötigt.