Techniklexikon

Klein-Gordon-Gleichung

^[n]Quantenmechanik, die relativistische Verallgemeinerung der freien Schrödinger-Gleichung für ein spinloses Teilchen der Masse m. Sie beruht auf der relativistischen Energieformel E² = p² + m² und auf dem quantenmechanischen Korrespondenzprinzip, also der Ersetzung des Impulses p durch den Operator  und lautet damit

angewandt auf eine Wellenfunktion .

Die allgemeine Lösung der Klein-Gordon-Gleichung setzt sich aus Lösungen zu positiver und negativer Energie k⁰ = ±w(k) zusammen (w(k) = (k²+m²)^{1 / 2}),

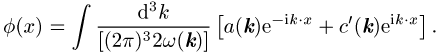
Die Quantisierung des Klein-Gordon-Feldes erfolgt durch Interpretation der Koeffizienten a(k) und c(k) als Erzeugungs- und Vernichtungsoperatoren  und , die die Vertauschungsrelationen

erfüllen (alle anderen Kommutatoren verschwinden) und mit denen man den Hilbert-Raum für beliebig viele Teilchen der Masse m aufbauen kann. Die Bedeutung der Klein-Gordon-Gleichung liegt jedoch vor allem darin, dass ihr alle relativistischen Wellenfelder genügen müssen (Quantenfeldtheorie).