Techniklexikon

Langevinsche Theorie des Paramagnetismus

Festkörperphysik, enthält Aussagen über das mittlere magnetische Moment ámñ = m ácosañ eines Dipols in einem Stoff unter dem Einfluss eines den Dipol orientierenden Magnetfeldes B (a: Winkel zwischen B und m) und der desorientierenden Wirkung der Wärmebewegung.

In klassischer Betrachtungsweise geht man von einer nach Boltzmann bestimmten Wahrscheinlichkeit für die Einstellung des magnetischen Dipols aus. Mit der Energie U = -m × B = -mB cosa eines Dipols im Feld wird ácosañ dann durch die klassische Langevin-Funktion L_¥(a) beschrieben:L_¥(a) = coth(a) - 1 / a, mit a = mB / kT (k: Boltzmann-Konstante, T: Temperatur). Die Magnetisierung von N Atomen im Volumen V ist dann M = (N / V)m ácosañ.

Berücksichtigt man die Tatsache, dass nach der Quantentheorie nur diskrete Einstellungsmöglichkeiten für die magnetischen Dipole bestehen, so erhält man mit einem Gesamtspin J für die Magnetisierung statt der Langevin-Funktion die Brillouin-Funktion.

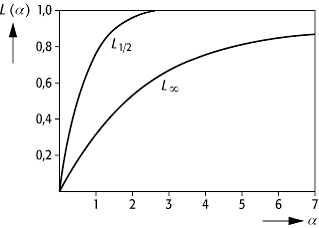
Langevinsche Theorie des Paramagnetismus: Alle Langevin-Funktionen liegen zwischen der Langevin-Funktion für den klassischen Grenzfall beliebiger Einstellungsmöglichkeiten der magnetischen Momente, L_¥(a), und der des quantenmechanischen Spezialfalls von nur zwei Einstellungsmöglichkeiten, L_{1 / 2}(a), bei der kein Bahnmoment vorhanden ist und das magnetische Moment nur durch den Elektronenspin gegeben ist.