Techniklexikon

Parton-Modell

Teilchenphysik, phänomenologisches Modell zur Erklärung des in der tiefinelastischen Elektron-Nukleon-Streuung beobachteten Skalenverhaltens (Bjørken-Scaling) der Formfaktoren. Ausgangspunkt ist die Annahme, dass die Streuung an punktförmigen Partonen unbekannten Spins, die jeweils einen Bruchteil x_i des Hadron-Viererimpulses p tragen und mit den Quarks identifiziert werden können, den Hauptbeitrag zum Hadron-Tensor  liefert. Jedes Parton wird durch eine Wahrscheinlichkeitsfunktionen  beschrieben (Parton-Verteilungsfunktion), die die Wahrscheinlichkeitsdichte dafür angibt, dass das i-te Parton einen Impulsanteil x trägt (). Bereits dieses sehr einfache Bild erklärt das Skalenverhalten: Aus der Impulserhaltung  (q: Impulsübertrag) folgt  (M: Ruhemasse des Nukleons, ) und damit im tiefinelastischen Bereich (), wo  und  vernachlässigt werden können,

was gerade das Skalenverhalten wiedergibt: alle Strukturfunktionen hängen nur noch von  ab.

Das Parton-Modell erlaubt ausserdem die Berechnung von Einschränkungen an die Formfaktoren W₁ und W₂, mit denen der Hadrontensor auf Grund allgemeiner Kovarianzforderungen ausgedrückt werden kann,

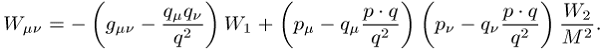
Jedes Parton liefert zum Hadrontensor

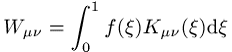
mit einer unbekannten Funktion f(x) den Beitrag

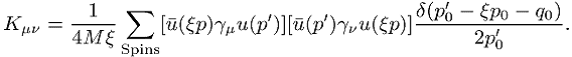
Die Deltafunktion kann unter Berücksichtigung der Eigenschaft  umgeschrieben werden in

woraus explizit die Identität x = x hervorgeht. Führt man die Spinsumme aus und integriert über x, erhält man

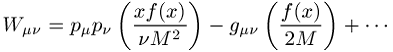
und damit aus dem Vergleich mit der allgemeinen Form von

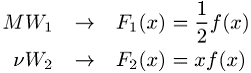
sowie die Callan-Cross-Relation

Dieses Ergebnis bestätigt auch den Spin 1 / 2 der Partonen: für Spin-0-Teilchen wäre .

Lässt man für die im Nukleon vorhandenen Quark-Partonen verschiedene Verteilungsfunktionen zu und schreibt F₁ in der Form

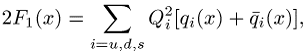
wobei Q_i die Ladung des i-ten Quarks ist, dann erhält man

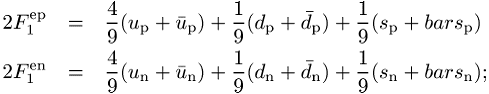
unter der Annahme der Isospinsymmetrie () folgt daraus die Relation

,

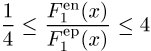die experimentell gut bestätigt ist.