Techniklexikon

Formfaktor

QuantenmechanikKernphysikTeilchenphysik^[n], elektromagnetischer Formfaktor, Strukturfunktion, F(q²), im nichtrelativistischen Fall die Fourier-Transformierte einer Ladungsverteilung r(r): F(q²) = òr(r)e^iqrd³r (Fourier-Transformation, q ist der übertragene Impuls). Formfaktoren spielen eine wichtige Rolle bei der Messung bzw. Berechnung von Wirkungsquerschnitten bei der Streuung an nichtpunktförmigen Teilchen wie Hadronen (z.B. das Proton p und das Neutron n) oder Mesonen (Streutheorie). Für eine punktförmige Ladungsverteilung r(r) = 1 / (4p)d(r) ist F(q²) = 1; für eine homogen geladene Kugel vom Radius R gilt F(q²) = 3b³(sinb - bcosb) mit b = 2p|V|R / h. Für q  0 ist F(q²) direkt proportional zu dem mittleren quadratischen Radius  der Ladungsverteilung.

Der experimentell bestimmte Wirkungsquerschnitt für ein Streuexperiment an Kernen oder Nukleonen kann als Produkt geschrieben werden aus einen Anteil, der die Wechselwirkung mit einem punktförmigen Teilchen beschreibt, und dem Formfaktor:

.

Typische Streuexperimente sind dabei die Elektron-Nukleon-Streuung und die Photoproduktion g + N  N + p. Wird das Nukleon dabei zunächst als punktförmig angenommen, so ergibt sich für den differentiellen Wirkungsquerschnitt der elastischen Streuung in das Raumwinkelelement dW:

,

mit E: Energie des einfallenden Elektrons im Ruhesystem (Laborsystem) des Nukleons, q = 2Q: Streuwinkel, M: Nukleonmasse, a: Feinstrukturkonstante. Für den Fall des Verschwindens des Quadrates des Impulsübertrages t = -q² = 4EE\'sin²Q (t heisst auch Mandelstamsche Variable), wobei E\' die Energie des gestreuten Elektrons ist, erhält man den Mottschen Streuquerschnitt (ds_el / dW)_Mott. Der Übergang zu einem Nukleon mit ausgedehnter Ladungsverteilung führt unter Ausnutzung der Lorentz-Invarianz und der Eichinvarianz der Streuamplitude auf die elektromagnetischen Formfaktoren G_e und G_m, man erhält dann die Rosenbluth-Formel (N.M. Rosenbluth, 1950):

 bzw.  ist der elektrische bzw. der magnetische Formfaktor des Nukleons. Mit den Indizes p für das Proton und n für das Neutron gilt  und  bzw.  und , wobei mp bzw. m_n das anomale magnetische Moment des Protons bzw. Neutrons in Einheiten von Kernmagnetonen ist.

Theoretisch werden Formfaktoren durch Vertexkorrekturen berechnet, z.B. wird so das anomale magnetische Moment des Elektrons in der Quantenelektrodynamik (QED) bestimmt: Der perturbative Elektron-Photon-Vertex kann durch die Gordon-Identität umgeformt werden, , wobei q = p¢ - p. Der zweite Term in diesem Ausdruck beschreibt im Ruhesystem des Elektrons die Kopplung des Spins zum Magnetfeld: . Hieraus ergibt sich ein gyromagnetisches Verhältnis von g = 2. Durch Einschleifen-Korrekturen bekommt man dagegen g = 2 + a / p und bis zur dritten Ordnung,

g/2 - 1 = a_th = 0,001 159 652 411(166). Es stimmt mit dem experimentellen Wert gut überein: a_exp = 0,001 159 652 209(31).

Aus den bei der tiefinelastischen Elektron-Nukleon-Streuung gemessenen Formfaktoren wurde das Partonmodell entwickelt. Weitere wichtige Anwendungen sind der Formfaktor des r-Mesons (Test der Vektor-Meson-Dominanz) und der des Pions (Ableitung der Goldberger-Treimann-Relation aus der PCAC-Hypothese). [BK1, UK]

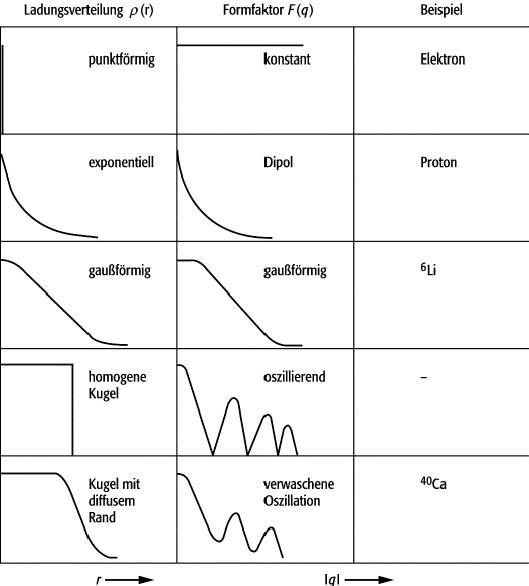
Formfaktor 1: Beispiele für Ladungsverteilung r(r) und zugehörigen Formfaktor F(r).

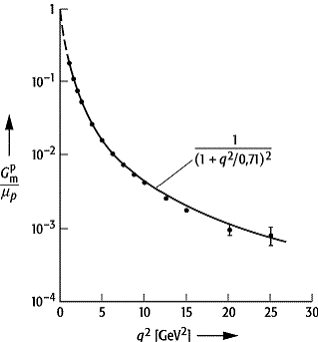
Formfaktor 2: elektromagnetischer Formfaktor  des Protons für hohe q². Die beobachteten Werte werden gut durch die angepasste Dipolgleichung beschrieben.

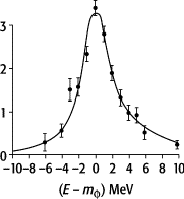
Formfaktor 3: elektromagnetischer Kaon-Formfaktor in der Nähe der Masse des f-Mesons m_f.