Techniklexikon

Relaxationsprozesse

Elektrodynamik und ElektrotechnikFestkörperphysik, allgemein verzögerte Reaktionen eines Systems auf eine äussere Einwirkung, die nach Ende der Einwirkung abläuft. Bei einmaliger Störung handelt es sich um eine während einer typischen Zeit, der Relaxationszeit, ablaufende Wiederherstellung des ursprünglichen Gleichgewichtszustandes; bei einer periodischen Störung ergibt sich eine Phasenverschiebung zwischen Störung und Systemantwort. Sind die Relaxationszeiten eines Systems kleiner als die für Zustandsänderungen typischen Zeiten, handelt es sich um ein nichtstatisches System, sind sie grösser, um ein quasistatisches. In der Thermodynamik behandelt man Relaxationsprozesse als irreversible Prozesse, sie sind eng mit Transportprozessen verwandt. Ein besonders wichtiges Forschungsgebiet für Relaxationsprozesse ist die dielektrische Relaxation. Viskoelastische Relaxation tritt bei viskoelastischen Flüssigkeiten, z.B. Polymeren, auf, welche unter konstanter Deformation eine abnehmende mechanische Spannung aufweisen. Der Elastizitätsmodul E nimmt dann exponentiell mit der Zeit ab: , wobei  die Relaxationszeit und  die Viskosität ist. Die Relaxationszeit ist ein Mass dafür, wie lange die Polymerkette braucht, um nach einer Streckung wieder in den verknäulten Zustand zurückzukehren, und wird hauptsächlich von der Masse des Moleküls bestimmt. Da in einem Polymer stets Moleküle unterschiedlicher Länge auftreten, sind die Relaxationsszeiten statistisch verteilt. Wird der Flüssigkeit keine Möglichkeit zur Relaxation gegeben - z.B. durch hochfrequente Deformationen mit einer Periode unterhalb der Relaxationszeit -, reagiert das System verstärkt elastisch, die Viskosität nimmt gleichzeitig ab.

Ferner sind die NMR-Relaxation und Relaxationsprozesse in der Rheologie von Bedeutung.

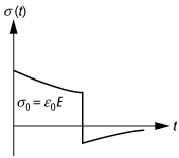
Relaxationsprozesse: Relaxationskurve eines viskoelastischen Stoffes; Bereich I: Dehnung = const., Bereich II: Dehnung geht sprunghaft auf Null.