Techniklexikon

Stark-Effekt

Atom- und Molekülphysik, die Aufspaltung und Verschiebung von Spektrallinien, die von Atomen emittiert werden, welche sich in einem elektrischen Feld befinden, benannt nach dem deutschen Physiker J. Stark, der dieses Phänomen 1913 zeitgleich mit L. Surdo erstmals beobachtete. Die Anwesenheit des elektrischen Feldes E (welches homogen über die Dimension eines Atoms sein soll und dessen Feldlinien in z-Richtung zeigen) bewirkt einen zusätzlichen Energieterm im Hamilton-Operator, , der als Störterm behandelt wird. Die Energieverschiebung auf Grund des elektrischen Feldes erhält man aus einer zeitunabhängigen Störungsrechnung. Der lineare Stark-Effekt, bei dem die Verschiebung der Energieniveaus proportional zur elektrischen Feldstärke ist, tritt nur bei (quasi-)entarteten Zuständen auf (quasi-entartet bezieht sich auf Fälle, in denen die Energieverschiebung durch das elektrische Feld viel grösser als die Feinstrukturaufspaltung des Zustandes ist), der Grundzustand des Wasserstoffatoms zeigt demnach keinen linearen Stark-Effekt. Dies ist mit der Beobachtung verknüpft, dass nur entartete Zustände ein permanentes elektrisches Dipolmoment besitzen können. Die Aufspaltung der vier entarteten Zustände des n = 2 Niveaus im Wasserstoffatom ist in Abb.1 dargestellt. Die Wellenfunktionen der drei Stark-Zustände sind keine Eigenfunktionen des Operators L² (l ist keine gute Quantenzahl), nur m_l bleibt gute Quantenzahl. Das elektrische Feld »mischt« also Zustände mit verschiedenen l, was man auch als »quenching« bezeichnet.

In wasserstoffähnlichen Atomen bewirkt der lineare Stark-Effekt des ersten angeregten Zustandes (n = 2) eine Verschiebung der Energien der Zustände y(n = 2, l, m_l = 0) um E⁽¹⁾ = ±3 eE a₀ / Z. Stark demonstrierte diesen Effekt anhand der Aufspaltung der Spektrallinien der Balmer-Serie (Balmer-Formel), wozu er elektrische Felder der Grössenordnung 10⁷V / m benötigte.

Der quadratische Stark-Effekt tritt dann auf, wenn das Atom kein permanentes Dipolmoment hat, vielmehr das elektrische Feld ein Dipolmoment induziert, das dann wiederum mit dem äusseren Feld wechselwirkt. Damit ist die Verschiebung der Energieniveaus proportional zum Quadrat der Feldstärke. Der quadratische Stark-Effekt ist ein Störungsterm zweiter Ordnung und ist daher sehr schwach. Die Energieverschiebung des Grundzustandes des Wasserstoffatoms beispielsweise beträgt DE⁽²⁾ = -2,25 (4pe₀) a₀³ / Z⁴E² = 0,0025 meV für E = 10⁸ V / m. Ein weiterer Effekt des elektrischen Feldes ist die »Verbiegung« des Coulomb-Potentials des Atomkernes (siehe Abb.2). Es entsteht eine Potentialbarriere, durch die vor allem Elektronen in höheren Anregungszuständen leicht hindurch tunneln können. Dies verkürzt die Lebensdauer dieser Zustände und erhöht damit die Linienbreite bei optischen Übergängen (DE ~ 1 / t), und es verschiebt die Seriengrenzen im Wasserstoffatom zu niedrigeren Energien.

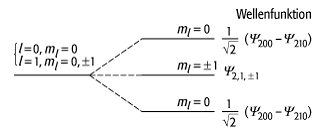
Stark-Effekt 1: Energieniveaus des n = 2 Zustandes des Wasserstoffatoms im elektrischen Feld. In Abwesenheit des Feldes sind die vier Unterzustände y_(2,0,0), y_(2,1,0), y_(2,1,1), y_(2,1,-1) entartet. Das elektrische Feld verschiebt die Energie der Zustände mit m_l = 0 und mischt Zustände mit unterschiedlichem l.

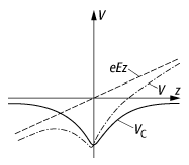
Stark-Effekt 2: Verformung des Coulomb-Potentials V_C durch ein elektrisches Feld E.