Techniklexikon

Variationsrechnung

Mathematische Methoden und Computereinsatz, Teildisziplin der Mathematik, die sich mit der Bestimmung von Funktionen (oft Kurven oder Flächen) beschäftigt, die ein bestimmtes Funktional, meist ein Integral, minimieren oder maximieren. Im Gegensatz zu Optimierungsproblemen mit endlich vielen Variablen handelt es sich hierbei um ein unendlich dimensionales Optimierungsproblem. Beispiel: Eine zu bestimmende Kurve sei von der Form  und rotiere zwischen  und  um die -Achse. Der Flächeninhalt der von der Kurve erzeugten Rotationsfläche, d.h. die Oberfläche des Rotationskörpers, bzw. das Flächenfunktional

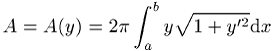
seien zu minimieren; die Lösung ist die Schar der Kettenlinien

mit  als Leitlinie und Konstanten  und . Als Beispiel eines dreidimensionalen Variationsproblems sei das Seifenhautproblem bzw. Plateaus Problem genannt: zu einer vorgegebenen geschlossenen Raumkurve ist diejenige Fläche mit kleinstem Inhalt zu bestimmen, die von dieser gegebenen Kurve berandet wird. Diese Fragestellung führt in der modernen Mathematik auf den Themenkomplex Minimalflächen.

Mit Hilfe der Variationsrechnung lassen sich eine Reihe physikalischer Gesetze aus der Minimierung geeigneter Funktionale aus einem Variationsprinzip gewinnen. Neben vielen geometrischen (z.B. Geodätenprobleme, d.h. Bestimmung kürzester Linien, Minimalflächen, etc.) und geometrisch-mechanischen Problemen (z.B. das 1696 von J. Bernoulli gestellte Problem der Brachistochrone) spielt die Variationsrechnung in technischen Problemen und der numerischen Mathematik eine Rolle und führt zur Disziplin der optimalen Steuerung (bei der im Gegensatz zur klassischen Variationsrechnung noch differentielle oder algebraische Nebenbedingungen auftreten). Die optimale Steuerung findet Anwendung z.B. bei der Berechnung der Bahnen künstlicher Himmelskörper, insbesondere bei der Bestimmung energieminimaler Bahnen von Raumsonden zu den äusseren Planeten.

Im einfachsten Fall ist ein stationärer Wert  des Integrals  zu bestimmen (siehe Abb.). Die Abbildung  wird auch Funktional genannt, wobei  einen näher zu spezifizierenden Funktionenraum bezeichnet. Technisch führt man dabei einen (kleinen) Parameter  ein, der die Lösung  in der Form  parametrisiert, wobei  eine beliebig oft differenzierbare Testfunktion darstellt. Die Stationarität des Integrals für die Lösung  wird damit aus der notwendigen Bedingung

gewonnen;  wird auch erste Variation des Integrals  genannt. Differentiation unter dem Integralzeichen, partielle Integration des zweiten Integranden und Berücksichtigung der Nebenbedingungen führt dann auf die Gleichung

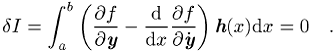
Da diese Integralbedingung für alle Testfunktionen  erfüllt sein muss , ist nach dem Fundamentallemma der Variationsrechnung (Satz von Du Bois-Reymond, 1879) ein Rückschluss auf den Integranden möglich. Dieses Lemma besagt nämlich, dass

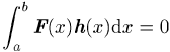
für alle  mit stetigen zweiten Ableitungen nur erfüllt sein kann, wenn  auf . Die notwendige Bedingung dafür, dass  ein Extremum annimmt, sind somit die Euler-Lagrange-Differentialgleichungen (ELD)

Diese Differentialgleichung zweiter Ordnung beinhaltet zwei willkürlich wählbare Konstanten, die z.B. an den beiden Endpunkten gewählt werden können. Da in den ELD die Ableitung der gesuchten Funktion auftaucht, spielt die Wahl des Funktionenraums  bzw. der Funktionenklasse eine offensichtliche Rolle. Bereits bei der Aufstellung des Funktionals sind Fragen der Integrierbarkeit zu klären. Lösungskurven, die sich aus den ELD ergeben, sind noch daraufhin zu untersuchen, ob die gefundene Funktion das Funktional wirklich minimiert und nicht vielleicht auf ein Maximum führt. Das bekannteste Beispiel in der Physik, das auf ein Variationsproblem führt, ist wohl das Hamiltonsche Prinzip der klassischen Mechanik, wobei die Funktion  durch die Lagrange-Funktion gegeben ist. Hier ergibt sich für die meisten physikalischen Probleme automatisch ein Minimum, da es nur eine stationäre Lösung gibt (Eindeutigkeits- und Existenzsatz gewöhnlicher Differentialgleichungen) und die Natur sich als kooperativ erweist: die so bestimmte stationäre und eindeutige Lösung minimiert tatsächlich das Wirkungsintegral.

Eine Erweiterung der bereits genannten Probleme ergibt sich, wenn neben dem zu minimierenden Zielfunktional ein weiteres Gleichungs- oder Ungleichungsfunktional tritt, also z.B.

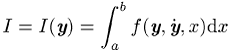
und

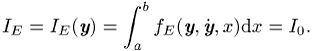
Hierzu zählen die bereits in der Antike bekannten isoperimetrischen Probleme, die eine Kurve bekannter Länge (Flächenumfang) so zu bestimmen suchen, dass die eingeschlossene Fläche minimal wird; die Lösung ist im einfachsten Fall ein Kreis, wie schon von Zenodoros gezeigt wurde. Im allgemeinen können die Probleme mit Hilfe der Lagrange-Funktion  gelöst werden, wobei die notwendigen Bedingungen, d.h. die ELD, dann für  gelten.

Während bei den klassischen Problemen der Variationsrechnung die Existenz der Lösung meist direkt aus der Anschauung oder aus der physikalischen Fragestellung garantiert werden kann, ist dies bei Variationsproblemen unter Nebenbedingungen weniger offensichtlich. Die Aufgabe, die kürzeste Verbindungskurve zwischen zwei Punkten zu bestimmen, die die Verbindungsgerade senkrecht schneidet, besitzt keine Lösung. Zwar ist die Länge der Verbindungsgerade eine untere Schranke, aber diese untere Schranke kann von keiner Kurve angenommen werden. Wesentlich komplizierter noch sind Variationsprobleme bei Gegebenheit von Variationsungleichungen. Hierzu stelle man sich z.B. eine beliebige nicht-konvexe ebene Fläche mit glattem Rand vor. Die kürzeste Verbindungslinie, die nicht innerhalb dieser Fläche verläuft und zwei Randpunkte der Fläche verbindet, wird im konvexen Teil der Fläche auf dem Rand verlaufen (Kontakt, aktive Ungleichung), ansonsten in nicht-konvexen Teilen den Rand aber nicht berühren (inaktive Ungleichung). Damit kommen zu den variationstheoretischen Aspekten topologische Fragestellungen und Methoden ins Spiel.

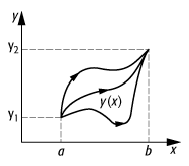
Variationsrechnung: Bestimmung der Kurve y(x), für die das Funktional extremal wird. Diese Kurve ist eingebettet in eine Schar von Vergleichskurven mit denselben Randwerten.