Techniklexikon

Vektorprodukt

Mathematische Methoden und Computereinsatz, Kreuzprodukt, dreidimensionaler Spezialfall des äusseren Produktes zweier Vektoren. Im  ist das Vektorprodukt zweier Vektoren x und y definiert als Vektor

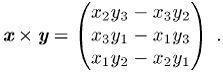
Sehr nützliche Eigenschaften des Vektorprodukts lassen sich aus der Darstellung in Form einer Determinante gewinnen:

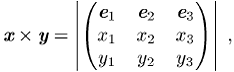
wobei  und  die Einheitsvektoren des  bezeichnen. Aus den Eigenschaften von Determinanten folgt z.B.  und daraus wiederum . Bezeichnet  den Winkel zwischen den Vektoren  und , so gibt

den Flächeninhalt des von  und  aufgespannten Parallelogramms an;  kann aus dem Skalarprodukt  berechnet werden. Das Vektorprodukt genügt den Relationen

und mit einem Skalar

Für die Physik wichtig ist die Produktregel hinsichtlich der Ableitung, d.h.

Schliesslich kann das Vektorprodukt wegen seines Verhaltens bei Spiegelungen aufgefasst werden als Pseudovektor bzw. Pseudotensor vom Rang 1, wobei dann gilt

Hierbei bezeichnet  das Levi-Civita-Symbol.