Techniklexikon

Bloch-Grüneisen-Gesetz

von F. Bloch und E. Grüneisen gefundener Zusammenhang, der den Beitrag der Elektron-Phonon-Wechselwirkung zum elektrischen Widerstand in regulären Metallen angibt. Für die Herleitung werden lediglich Normal-Prozesse, jedoch keine Umklapp-Prozesse berücksichtigt. Weiterhin wird für das Elektronensystem eine isotrope Verteilung der Elektronenzustände (sphärische Fermi-Fläche) gefordert, das Phononensystem soll stationär sein, das Debye-Modell wird angewendet, und der optische Zweig der Dispersionsrelation wird vernachlässigt.

Unter diesen Bedingungen wird durch Lösen der Boltzmann-Gleichung folgender Ausdruck für den spezifischen Widerstand r gefunden:

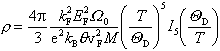  (1)

(k_F: Radius der Fermi-Fläche, E_F: Fermi-Energie, k_B: Boltzmann-Konstante, _F: Geschwindigkeit der Elektronen auf der Fermi-Fläche, W₀: Volumen der Elementarzelle, M: Masse eines Metallatoms, Q_D: Debye-Temperatur). Der Ausdruck I₅ steht für das Integral

.

Hierfür können für hohe und tiefe Temperaturen einfachere Grenzgesetze angegeben werden. Für T  >> Q_D ist I₅ » , für den elektrischen Widerstand ergibt sich daraus r ~ T/Q_D². Dieses lineare Temperaturverhalten des Widerstandes wird bei vielen Metallen im Raumtemperaturbereich beobachtet. Für T << V_D ergibt das Integral den konstanten Wert 124,4, es folgt r ~ T⁵/Q_D⁶. Dieses Ergebnis wird auch T⁵-Gesetz des elektrischen Widerstandes für tiefe Temperaturen genannt. Auch dieses Gesetz ist für viele Metalle experimentell bestätigt worden. Besonders bei Übergangsmetallen finden sich jedoch z.T. beträchtliche Abweichungen. Diese können durch einen in T quadratischen Term beschrieben werden, der den Beitrag der Elektron-Elektron-Stösse zu r beschreibt.

Wird Gleichung (1) durch r(Q_D) dividiert, so ergibt sich ein für alle Temperaturen gültiger Ausdruck für den reduzierten spezifischen Widerstand in Abhängigkeit von T/Q_D:

.

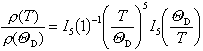Wird r bei zwei Temperaturen T₁, T₂ mit T₁ << V_D << T₂ bestimmt und der Quotient  gebildet, so kann hieraus die Debye-Temperatur experimentell bestimmt werden. Es ergibt sich für viele Metalle eine befriedigende Übereinstimmung mit den aus der spezifischen Wärmekapazität abgeleiteten Werten. [JH]