Techniklexikon

Duffing-Oszillator

Nichtlineare Dynamik, Chaos, Fraktale, Duffing-Schwinger, ein gedämpftes, schwingfähiges dynamisches System, das von einer nichtlinearen Kraft periodisch angetrieben wird, z.B. ein Drehpendel mit Unwucht (Abb.). Die Bewegungsgleichung lautet  (mit x, t: Orts- bzw. Zeitkoordinate, m: Masse, D, E: Konstanten der nichtlinearen Rückstellkraft, k: Dämpfungskonstante, F, w: Amplitude und Frequenz der Erregerkraft). Je nachdem, welche Werte die Parameter einnehmen, kann das System periodisches, bistabiles oder chaotisches Verhalten zeigen (Chaos). Eine der Ursachen hierfür ist die Interferenz von (sehr langem) Einschwingvorgang und erzwungener Schwingung. Der Duffing-Oszillator ist ein gutes Beispiel für einen Übergang ins Chaos gemäss der Feigenbaum-Sequenz (Wege ins Chaos).

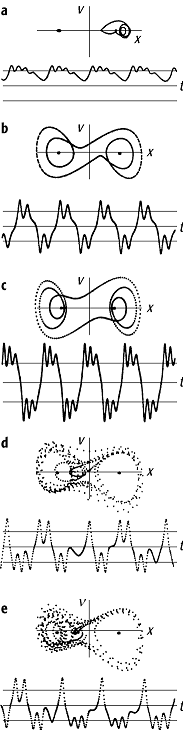
Duffing-Oszillator, Drehpendel mit Unwucht als Beispiel für einen Duffing-Oszillator. Dargestellt sind die Phasentrajektorie v(x) (oben) und der Schwingungsverlauf x(t) (unten), jeweils nach einem Einschwingvorgang von 200 Perioden. a) Bei kleiner Erregeramplitude schwingt das Rad um eine Gleichgewichtslage, bei grösseren Werten wird das Verhalten bistabil ( b), c)). d) und e ) zeigen chaotisches Verhalten und eine hohe Empfindlichkeit gegen die Anfangsbedingungen (die Anfangsausschläge unterscheiden sich nur um 0,2 %).