Techniklexikon

Heisenbergscher Hamilton-Operator

Operator, der die Energiezustände eines Spinsystems mit Heisenberg-Austausch beschreibt; er ist gegeben durch

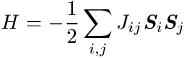
Die Summe erstreckt sich über alle wechselwirkenden Atome i und j mit den vektoriellen Spinoperatoren S_i = (S_ix,S_iy,S_iz) bzw. S_j = (S_jx,S_jy,S_jz), J_i,j ist das Austauschintegral. Je nach Gesamtenergie, die vom Vorzeichen der Austauschintegrale abhängt, ist die parallele (ferromagnetische Ordnung) oder antiparallele Ausrichtung (antiferromagnetische bzw. ferrimagnetische Ordnung) der Spins energetisch günstiger. Führt man für zwei Atome i und j den Gesamtspin S = S_i + S_j ein, so erhält man als Erwartungswert für einen Summanden

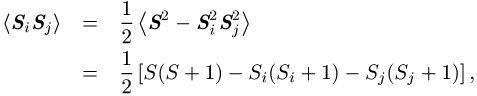
wobei die Spinquantenzahl von S die Werte S_i + S_j - 1, S_i + S_j - 2, ..., S_i - S_j, also insgesamt 2S_j + 1 Werte annehmen kann.  hat den grössten Wert bei Parallelstellung (S = S_i + S_j) und den kleinsten Wert bei Antiparallelstellung (S = S_i - S_j ), so dass bei positivem J_i,j die ferromagnetische Ordnung und bei negativem Austauschintegral die antiferromagnetische Ordnung den Grundzustand darstellt. In einem externen Magnetfeld H muss noch der Term -gm_BH · S_i (g: g-Faktor, m_B: Bohrsches Magneton) berücksichtigt werden.