Techniklexikon

Hyperfeinstruktur

HFS, die über die Feinstruktur hinausgehende zusätzliche Aufspaltung der Spektrallinien von Atomen oder Molekülen. Die Hyperfeinstrukturaufspaltungen sind etwa um den Faktor 10^-3 kleiner als die Feinstrukturaufspaltungen und liegen damit im Energiebereich 10^-5 eV. Die Hyperfeinstruktur wird durch zwei verschiedene Erscheinungen bewirkt:

1) durch die Wechselwirkung der Elektronen mit Kernmomenten. Unter Kernmomenten sind dabei die magnetischen (Dipol-)Momente der Atomkerne und die weniger wichtigen elektrischen Quadrupolmomente zusammengefasst. Die Quadrupolmomente resultieren aus einer Abweichung der Kernform von der Kugelgestalt;

2) durch Isotopieverschiebungen in Atomspektren. Hierbei handelt es sich nur um eine Aufspaltung der Linien bei einem Isotopengemisch, nicht um einen das einzelne Atom betreffenden Effekt.

Am besten geeignet für Untersuchungen der Hyperfeinstruktur ist das Fabry-Pérot-Interferometer. Mit Hilfe der Atomstrahlresonanzmethode können die Hyperfeinstrukturaufspaltungen direkt ausgemessen werden.

Die Hyperfeinstruktur (ohne Isotopieverschiebung) tritt bei den Spektrallinien aller Atome auf, deren Kern eine ungerade Massezahl aufweist, und ausserdem bei ²D und ¹⁴N, das sind alle Kerne mit von null verschiedenem Kernspin. Hauptursache der Hyperfeinstruktur ist die Wechselwirkung der Hüllenelektronen mit dem magnetischen Dipolmoment des Atomkerns. Da diese Kernmomente etwa um den Faktor 10^-3 kleiner als die Hüllenmomente sind, ist auch die gesamte Hyperfeinstrukturaufspaltung um diesen Faktor kleiner als die Feinstruktur. Die Richtung des Kernmoments ist durch den Kernspin I, die Grösse und Richtung des von den Elektronen am Kernort erzeugten Magnetfelds H durch den Gesamtdrehimpuls J der Hülle bestimmt. Bei der Kopplung von I und J zum gesamten Atomdrehimpuls F - entsprechend dem Vektormodell und völlig analog zur Kopplung von L und S bei der Russell-Saunders-Kopplung zur Deutung der Feinstruktur - hat die magnetische Wechselwirkungsenergie nach der Gleichung  verschiedene Werte für die unterschiedlichen Einstellungen von Kern- und Hüllenspin zueinander. Es bedeuten m_I das Kernmoment, m_K das Kernmagneton, g den gyromagnetischen Faktor des Kerns, I die Quantenzahl des Kernspins. Alle Terme eines Hyperfeinstruktur-Multipletts haben gleiche Quantenzahlen I und J, aber verschiedene Quantenzahlen F des gesamten Atomdrehimpulses, die alle ganz- oder halbzahligen Werte zwischen  und (J + I) durchlaufen. Die beobachteten Komponenten entsprechen der Auswahlregel DF = 0 oder ±1; 0 - 0 verboten. Die Analyse der gemessenen Hyperfeinstrukturaufspaltungen liefert die Quantenzahl des Kernspins I, ausserdem die magnetischen Momente bzw. den gyromagnetischen Faktor der Kerne, wenn das Magnetfeld der Elektronenhülle am Ort des Kerns bekannt ist. Es wird mit Hilfe spektraler Daten berechnet.

Bei nichtkugelförmigen Kernen tritt eine weitere, zum elektrischen Quadrupolmoment Q der Kerne und zu  proportionale Aufspaltung auf, aus deren Grösse Q bestimmt werden kann. Dazu sind allerdings Informationen über die Inhomogenität des elektrischen Feldes am Kernort erforderlich, die nur mit geringer Genauigkeit durch theoretische Berechnungen erhalten werden können.

In einem äusseren Magnetfeld präzessiert der Gesamtdrehimpuls F um die Feldrichtung in 2F + 1 verschiedenen Einstellungen, solange die magnetische Zusatzenergie klein ist gegenüber der feldfreien Hyperfeinstrukturaufspaltung. Wegen ihrer Kleinheit tritt aber schon bei relativ schwachen Feldern Entkopplung von J und I auf. Es ergibt sich ein partieller Paschen-Back-Effekt (auch Back-Goudsmit-Effekt genannt): Die Komponenten des anomalen Zeeman-Effekts der Feinstruktur (m_I) zeigen eine Aufspaltung in 2I + 1 äquidistante Komponenten in der Grössenordnung der feldfreien Hyperfeinstruktur.

Die Messungen des Zeeman-Effekts der Hyperfeinstruktur erlauben eine Bestimmung von I; eine zusätzliche Information über das magnetische Kernmoment erbringen sie nicht.

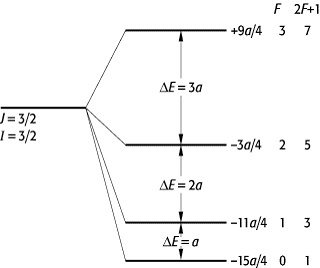
Hyperfeinstruktur: Hyperfeinaufspaltung eines Zustands mit J = 3 / 2 und I = 3 / 2. Rechts sind die Zahlenwerte der Quantenzahl F sowie der Grad 2F + 1 der Entartung nach m_F angegeben.